Prérequis:
- Cours sur les types abstraits
Ce cours comporte plusieurs pages:
Structure linéaire : La Pile
Les structures de données
Un premier exemple
La pile est une manière de ranger les données.
Elle correspond exactement à l’image traditionnelle d’une pile de cartes ou d’assiettes posée sur une table. En particulier, on ne peut accéder qu’au dernier élément ajouté, qu’on appelle le sommet de la pile.
L’illustration suivante montre que c’est la structure de données à adopter si l’on veut sortir d’un labyrinthe…
parcours pour sortir d'un labyrinthe
modelisation d'un labyrinthe
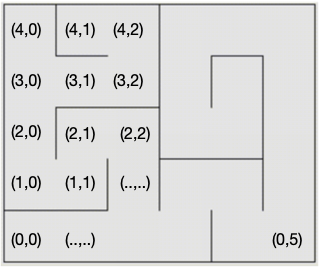
(4,0), (3,0), (3,1), (3,2), (4,2), (4,1) …
puis le chemin inverse jusqu’au sommet (3,0) :
(4,2), (3,2), (3,1), (3,0), …
Une fois revenu au sommet (3,0), on reprend l’exploration vers (2,0), (2,1),…
Il s’agit d’une méthode d’exploration du labyrinthe de type parcours en profondeur. L’algorithme est expliqué en détail à la page : SNT algorithmes graphe : parcours en profondeur
fil d'ariane
Lorsqu’elle s’avance plus en profondeur dans le labyrinthe, vers des sommets encore non explorés, elle empile.
Lorsqu’elle revient sur ses traces, elle dépile (elle retire des sommets de la pile).
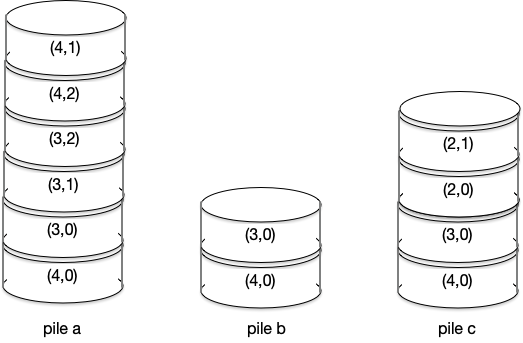
pile de sommets du labyrinthe
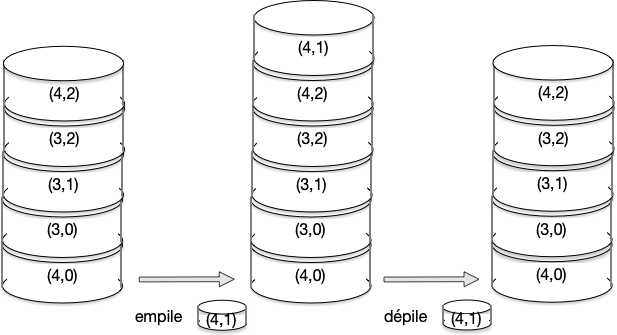
Elle revient jusqu’à (3,0).
Après avoir dépilé (4,1),(4,2),(3,2),(3,1), la pile est alors la pile b.
Puis, lorsqu’elle est parvenu à une bifurcation vers une nouvelle direction, elle poursuit son exploration (et empile à nouveau) : pile c. Qu’il faudra encore prolonger pour atteindre la sortie (en bas à droite).
pile du parcours en profondeur
Deuxieme exemple : une expression correctement parenthésée
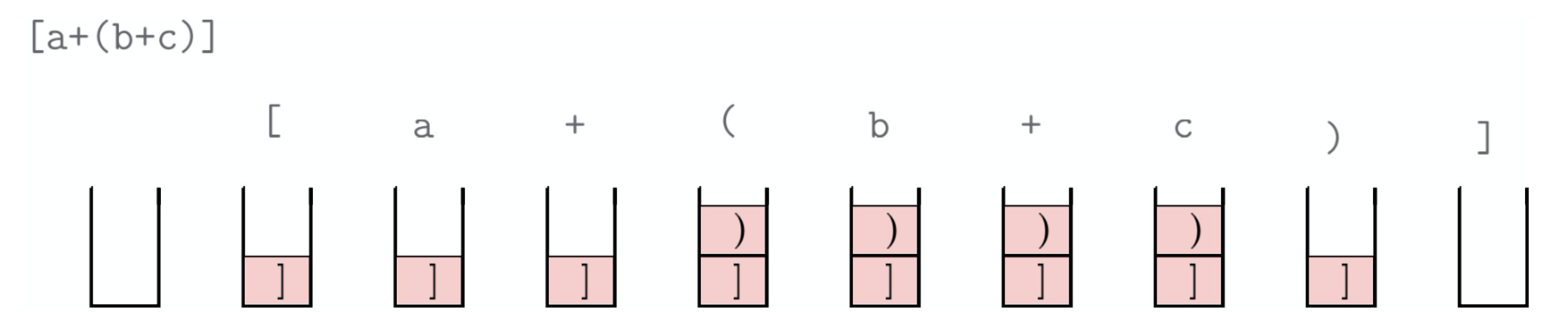
Principe : On lit l’expression de gauche à droite et on empile au fur et à mesure les caractères ouvrants : [, {, (. On dépile lorsqu’on lit le caractère fermant correspondant. A la fin, la pile doit être vide.
Dans l’exemple suivant, on voit que l’expression [a+(b+c)] est correctement parenthesée. Ce qui ne serait pas le cas pour [a+(b+c]).
Définitions
La pile: interface
La pile est une structure de données appropriée quand :
- On veut stocker des éléments dont le nombre est variable, et inconnu à l’avance.
- On peut ou on doit se contenter d’accéder au dernier élément stocké.
Dans d’autres cas, il faudra utiliser une autre structure de données, comme par exemple un tableau.
Une Pile est une structure de données linéaire (les données sont rangées sur un ligne ou une colonne). Le dernier élément entré sera aussi le premier à sortir (Last In First Out : LIFO).
Les méthodes (= fonctions) disponibles pour cette structure sont :
Implémenter un pile en Python
Le type List en Python possède déjà toutes les méthodes d’une pile :
pile = [] # creation d'une pile
pile == [] # tester si la pile est vide
pile.append(valeur) # empile valeur dans la pile
pile.pop() # depiler l'element au sommet
pile[-1] # lire l'element au sommet de la pile
Lorsque l’on fait référence à une structure de données de type pile en traduisant un algorithme en Python, il faudra se contenter de ces 5 instructions.
Interface ou implémentation ?
Les types abstraits, comme les piles, sont définis par leur interface (comment on s’en sert) plutôt que par leur implémentation (comment ils fonctionnent). Ils permettent d’étudier des algorithmes indépendamment du langage utilisé.
On verra ici deux manières d’implémenter la pile.
Créer ses propres fonctions
Pour traduire un algorithme utilisant cette structure pile, il peut être préférable de définir des instructions portant les noms de ces 5 instructions:
def Pile():
"""creation d'une pile vide à l'aide de l'instruction :
pile = Pile()
"""
return []
def est_vide(pile)
# à compléter
def empile(valeur,pile):
# à compléter
def depile(pile):
# à completer
def sommet(pile):
# à completer
Définir sa propre pile (construction d’un objet de type pile)
On peut créer un type (= une classe) Pile personnelle en Python.
Les méthodes (fonctions) déclarées précédemment sont alors associées à l’objet Pile. L’appel d’une méthode se fait à l’aide de l’instruction :
pile = Pile()
pile.est_vide()
pile.empile(valeur)
pile.depile()
pile.sommet()
Voir le cours sur la programmation orientée objet.
Rappel : Objet = type mutable. Quelle que soit la façon avec laquelle la pile est implémentée, il faudra se souvenir que celle-ci est un objet mutable. Cela a des conséquences sur la manière avec laquelle la pile est passée en argument d’une fonction, et comment cette fonction modifie la pile.
Pile et recursivité
Tout algorithme récursif peut être mis sous forme d’algorithme itératif avec une structure de données en pile.
Voir le cours sur la recursivité
Exercices sur les piles
Exercice 1 : implementer une pile
- Programmer les fonctions qui implémentent la pile:
Pile,est_vide,empile,depile,sommet. (editeur python en fin d’exerice) - Tester votre implémentation pour resoudre l’exercice suivant: (utiliser l’editeur python):
- Soit une liste L = [“a”,1,“b”,2,“c”,3,“d”,4]
- Parcourir les éléments de la liste L avec une boucle bornée
- empiler tous les nombres entiers dans une pile
p.
- empiler tous les nombres entiers dans une pile
Exercice 2 : lever des exceptions
Certaines des fonctions que vous avez écrites vont lever des exceptions dans le cas où la pile est vide.
- Pour ces fonctions, ajouter des instructions pour lever les exceptions dans le cas où la pile est vide. (utiliser l’editeur python de l’exercice 1)
- Tester vos fonctions avec une pile vide.
Exercice 3 : déverser une pile
Méthode itérative
Dans l’editeur de l’exercice 1:
Ecrire une fonction deversepile qui déverse une pile p1 dans une pile p2.
Cette fonction sera utilisée de la manière suivante : On utilise une pile intermédaire p3 :
p1,p2,p3=Pile(),Pile(),Pile()
deversepile(p1,p3)
deversepile(p3,p2)
Les fonctions que vous pourrez utiliser pour les piles seront celles définies dans l’exercice 1 : Pile,est_vide,empile,depile,sommet.
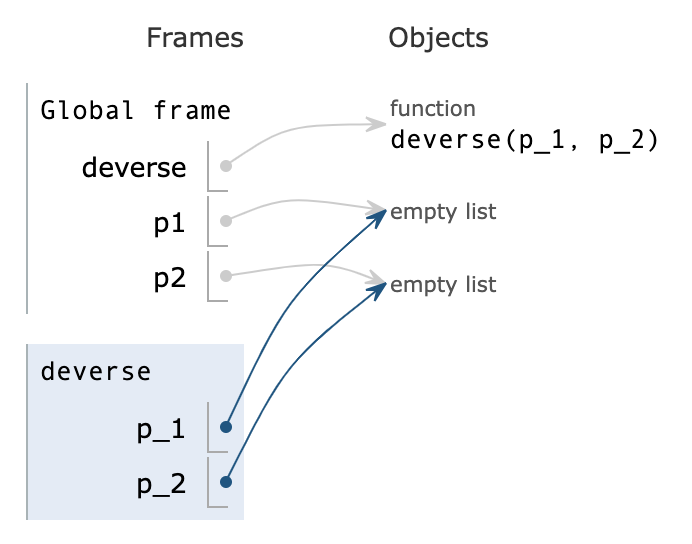
Visualiser sur Pythontutor
Ouvrir l’editeur pythontutor et executer le script pas à pas.
cliquer pour ouvrir sur pythontutor
Remarquez-vous?
- le dépilement retourne l’élément au sommet de
p1, tout en supprimant ce sommet - les éléments se rangent en sens inverse dans
p2avec l’empilement - la fonction ne retourne rien. Les listes
p1etp2sont modifiées par effet de bord, dans la fonction.
Exercice 4 : Evaluation d’une opération en notation polonaise inversée
Principe
la notation polonaise inversée permet d’écrire une opération sans utiliser de parenthèses. Il faut alors écrire les 2 opérandes avant l’opérateur. L’opérateur se trouve à droite des 2 opérandes.
En parcourant l’expression de gauche à droite, chaque fois que l’on rencontre un opérateur, on remonte vers la gauche pour rechercher les 2 opérandes et on remplace les 3 termes (2 operandes et 1 opérateur) par le resultat de l’opération.
On peut utiliser une pile pour réaliser la séquence de calculs.
Exemple : 1 2 + 4 * 3 +
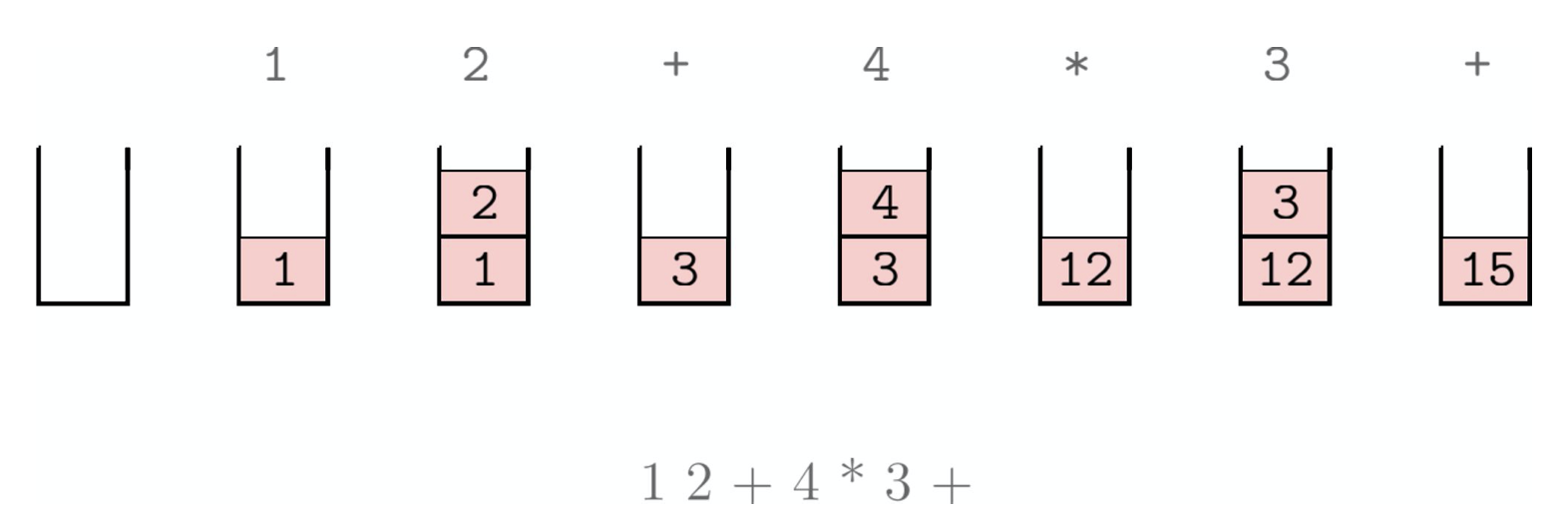
Arnaud Bodin : Calculatrice polonaise - les piles
Questions
- Compléter les fonctions
add,soust, etmultipqui doivent additionner, soustraire, et multiplier les arguments x et y. - Testez vos fonctions à l’aide du tableau associatif: Executer en console l’instruction:
dicoP['-'](3,4)qui doit renvoyer … -1 - Compléter la fonction evalNPI: Dans une boucle bornée qui parcourt tous les éléments de la liste L:
for a in L:
- si
aest un entier: empiler a dans une listepqui sera utilisée comme une pile. - si
aest un opérateur présent dans le tableau associatifdicoP:- depiler
pdeux fois et stocker les valeurs dans les opérandes x et y. - empiler la valeur calculée dans la pile
p
- depiler
- retourner la valeur finale stockée dans
p
Variante utilisant les fonctions lambda
On peut racourcir l’écriture du script en utilisant des fonctions lambda. Elles utilisent des paramètres pour calculer une valeur de retour, comme une fonction. Elles ne peuvent contenir qu’une expression.
On les déclare de la manière suivante:
lambda arguments: expression
Exemple 1:
sum = lambda a,b : a+b
Ces fonctions peuvent ne pas être nommées. On les place alors dans une liste, ou un dictionnaire.
dico = {'+' : lambda x,y : x+y,
'-' : lambda x,y : x-y,
'*' : lambda x,y : x*y
}
On calcule alors avec cette fonction en faisant: dico[a](3,4) par exemple:
Exemple 2:
a = '+'
if a == '+':
r = dico[a](3,4)
print(r)
# affiche 7
L’interêt des fonctions lambda est surtout de rendre le script plus lisible. Cela donne une autre option d’écriture.
Exercice 5: Reduction d’une chaine de caractères
Enoncé à la page suivante
Correction des exercices
Exercice 1
# exercice 1
L = ['a',1,'b',2,'c',3,'d',4]
def Pile():
return []
def est_vide(pile):
return pile == []
def depile(pile):
assert pile != [], 'impossible de depiler : pile vide'
return pile.pop()
def empile(a,pile):
pile.append(a)
def sommet(pile):
assert pile != [], 'la pile n_a pas de sommet : pile vide'
return pile[-1]
p = Pile()
for a in L:
if isinstance(a,int):
empile(a,p)
print(p)
Exercice 2
Les modifications ont été faites directement dans le corrigé de l’exercice 1.
Tester le script suivant à la suite de celui de l’exercice 1:
# exercice 2
p2 = Pile()
depile(p2)
Autres structures linéaires
Lien vers la page Listes et Files
Liens
- cours sur info.blaisepascal.fr
