Le cours comprend:
- une partie 2: Suite du cours sur la recursivité
- une page d'exercices
Récursivité
Principe
Un algorithme récursif est un algorithme qui fait appel à lui-même dans le corps de sa propre définition. Ce principe est aussi appelé : de l’autoréférence. (traité dans la partie autres applications de la page 2 du cours).
Cependant, cette premiere definition pourrait faire penser qu’une fonction récursive va s’appeler indéfiniment, et créer sans arrêt les mêmes figures, ou les mêmes traitements.

Ce n’est pas tout à fait cela.
Pour une fonction récursive, il y a plus que de la simple autoréférence:
-
Il y a transmission de valeurs entre 2 étapes de la pile d’appels recursifs. Une valeur va remonter d’un niveau $n$ vers le niveau $n-1$ qui l’a appelé.
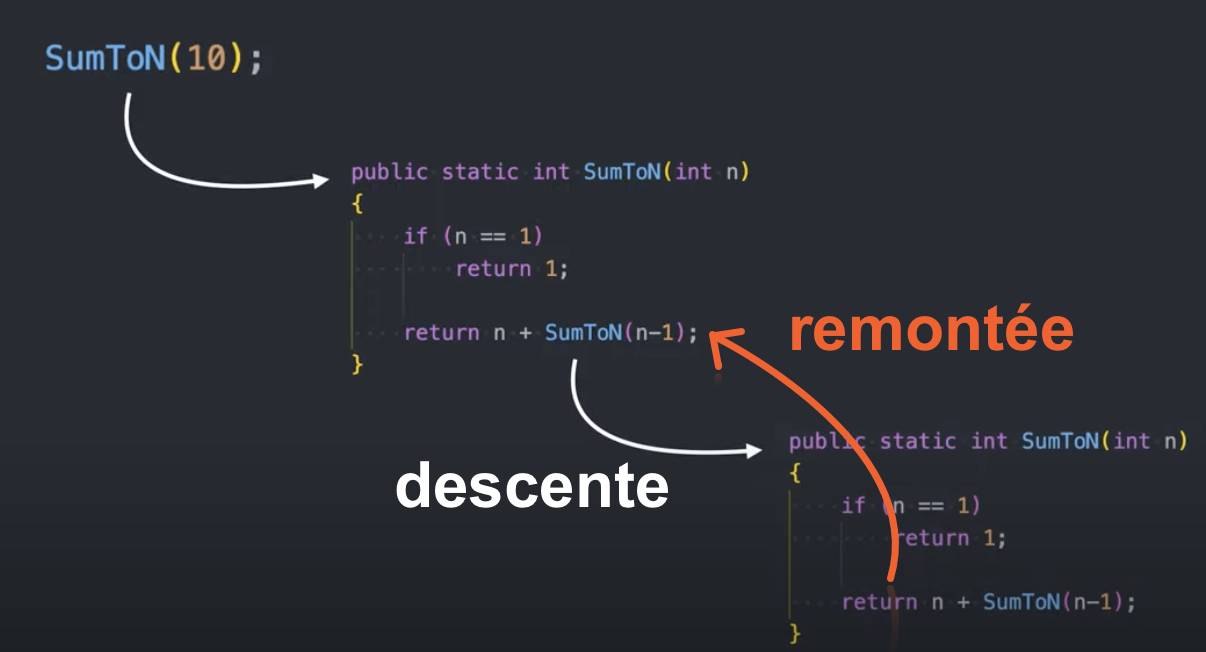
-
On remonte la pile d’appels parce que la fonction contient une condition de fin (appelée condition de base).

- enfin, les traitements ne sont pas tous identiques parce les arguments de la fonction changent à chaque nouvel appel recursif.
Analyse d’un exemple: itératif => récursif
Considérons une fonction ajoute2_iter qui prend N comme paramètre, et qui ajoute N fois 2.
Algorithme itératif
Supposons que nous souhaitions éviter la multiplication. L’algorithme itératif utilisera alors une boucle bornée:
def ajoute2_iter(N):
"""ajoute 2 un nombre N de fois
"""
s = 0
for i in range(N):
s = s + 2
return s
Résultat
>>> ajoute2_iter(10)
20
Algorithme récursif
Rappel de math: Une suite est une succession ordonnée d’éléments pris dans un ensemble donné.
On a la relation de récurence sur les éléments de la suite $u_n$:
$$u_{n+1} = 2 + u_n$$
ou encore:
$$u_{n} = 2 + u_{n-1}$$
On va adapter cette dernière relation dans l’appel de la fonction:
def ajoute2(N):
"""fonction qui s'appelle elle-meme N fois
"""
if N==0 :
return 0
else:
return 2 + ajoute2(N-1)
Résultat
>>> ajoute2(10)
20
Principe d’un algorithme récursif
L’algorithme récursif comprend 2 parties importantes:
- La Base : c’est le cas pour lequel le problème se resoud immediatement, par exemple :
if N==0 :
return 0
dans le script ajoute2: le problème se resoud immediatement pour N == 0).
- L’Hérédité : calcul à partir de paramètres plus “petits” :
return 2 + ajoute2(N-1).
Une définition plus générale serait que, pour l’hérédité, il y a un appel recursif avec un argument qui se rapproche plus de la condition de base.
def fonction_recursive(param):
if <cas de base> :
return value
else:
# instructions
fonction_recursive(f(param))
Remarque: Une instruction conditionnelle est incluse dans le corps de la fonction pour forcer la fonction à retourner sans que l’appel de récurence soit exécuté (La Base). Sans cela, le programme pourrait tourner en boucle…
Comparatif itératif - récursif
Une grande partie des problèmes peut se résoudre avec une implémentation récursive, comme avec une implémentation itérative. L’une ou l’autre peut paraître plus ou moins naturelle suivant le problème, ou suivant les habitudes du programmeur.
| Itératif | Récursif | |
|---|---|---|
| Principe | Permet d’executer plusieurs fois l’ensemble des instructions | La fonction s’appelle elle-même |
| Format | L’itération comprend l’initialisation, la condition, l’exécution de l’instruction dans une boucle et la mise à jour (incrémenter et décrémenter) la variable de contrôle. | Seule la condition de terminaison est spécifiée. |
| Terminaison | L’instruction d’itération est exécutée plusieurs fois jusqu’à ce qu’une certaine condition soit atteinte. | Si la fonction ne converge pas vers une condition appelée (cas de base), elle conduit à une récursion infinie. |
| Taille du script | L’itération rend le script plus long | Taille du script réduite |
Enfin, l’algorithme récursif utilise une pile d’appels, comme vu sur l’animation suivante:
animation issue de la page lyceum > recursivite (B. Abel)
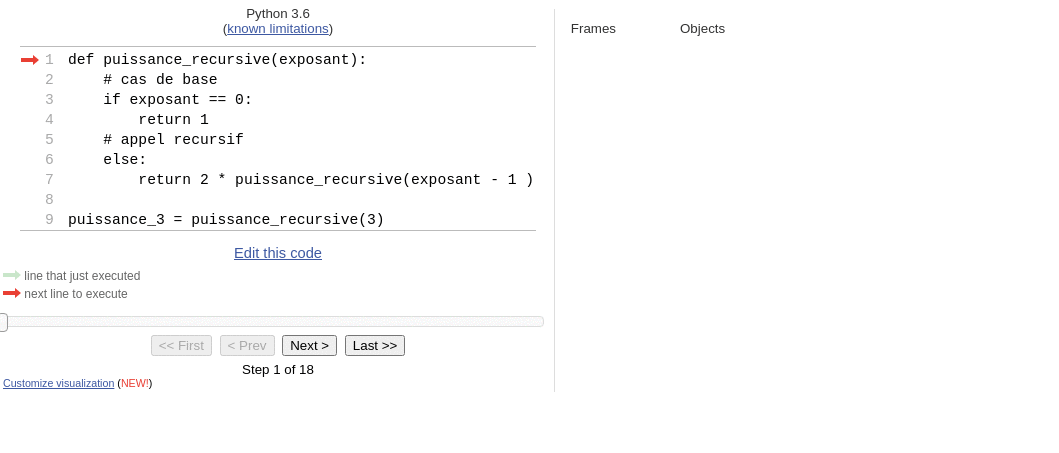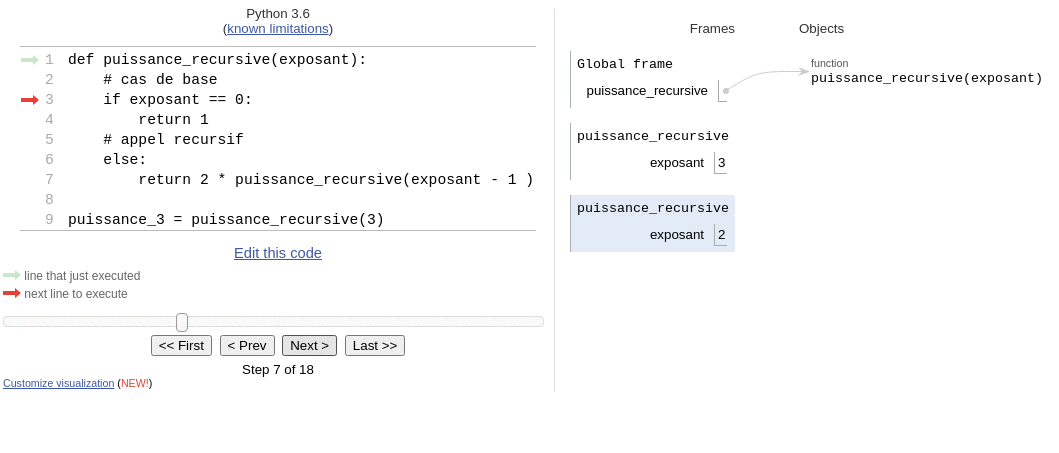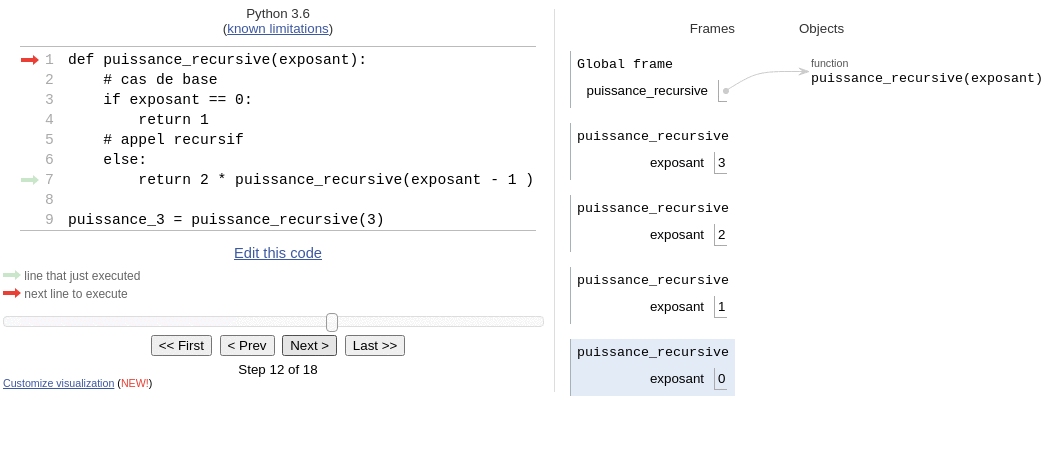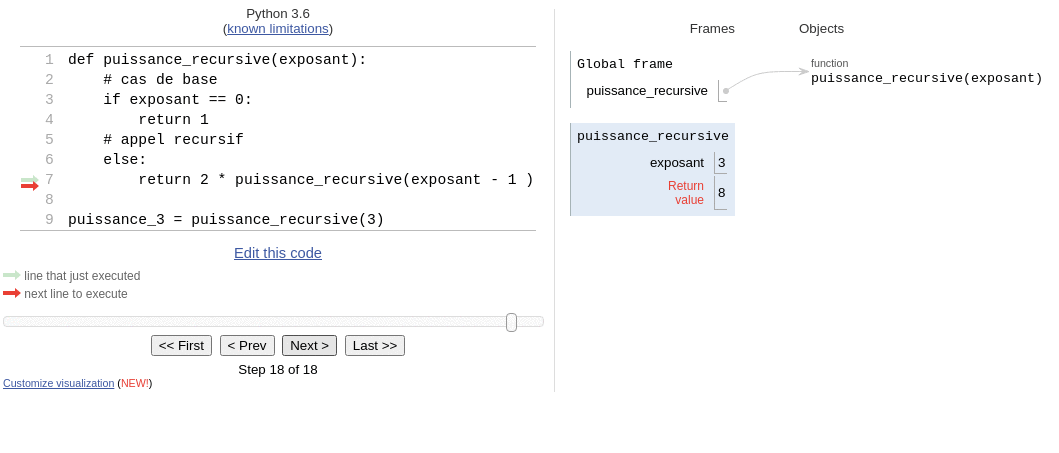
- factorielle
- suite de Fibonacci.
exemple : factorielle
programme itératif
def fact(n):
res = 1
for i in range(1,n+1):
res=res*i
return res
terminaison: l’algorithme consiste en une boucle qui execute n itérations. Le convergent n-i decroit strictement à chaque itération et on sort de la boucle quand il vaut 0.
Chaque iteration contient un nombre fini d’opérations élémentaires : 1 mutiplication et 1 affectation. Donc il termine après 2n+1 operations.
correction (ou validité): On prouve par recurrence sur le nombre d’iterations qu’apres la ieme iteration de la boucle for : res=i!
Preuve par récurrence: après la 1ere itération, res = 1 ! (OK)
Hypothèse de récurrence : (H.R.) supposons qu’après la ieme itération, res=i ! Montrons qu’après la (i+1)ieme iteration, res=(i+1)! :
avant la (i+1)e iteration, res = i !
La (i+1)e iteration multiplie res par i+1, donc après la (i+1)e iteration, $$res= i! \times (i+1) = (i+1)!$$
Après n iterations, res contient n ! donc le resultat est celui attendu.
Programme recursif
On a la relation de récurence suivante:
$$u_n = n \times u_{n-1}$$
La relation d’heredité est alors return n*fact_recur(n-1)
Le premier terme est:
$$u_0 = 1$$
et le script de la fonction recursive:
def fact_recur(n):
if (n==0) :return 1 else: return n*fact_recur(n-1)
On pourrait représenter la pile d’execution de cette fonction de la manière suivante :
Appel à fact_recur(4)
| 4*fact_recur(3) = ?
| Appel à fact_recur(3)
| | 3*fact_recur(2) = ?
| | Appel à fact_recur(2)
| | | 2*fact_recur(1) = ?
| | | Appel à fact_recur(1)
| | | | 1*fact_recur(0) = ?
| | | | Appel à fact_recur(0)
| | | | Retour de la valeur 1
| | | | 1*1
| | | Retour de la valeur 1
| | | 2*1
| | Retour de la valeur 2
| | 3*2
| Retour de la valeur 6
| 4*6
Retour de la valeur 24
Dans le cas d’un algo recursif, pas de convergent ni d’invariant de boucle. On prouve par recurrence sur n.
Teminaison: si n=0, fact(0) fait un test et renvoie 1, sans appel recursif.
Hypothèse de récurrence: fact(n) termine après n appels recursifs. Montrons que fact(n+1) termine après (n+1) appels recursifs.
fact(n+1) fait un test n+1>0 donc on passe au else puis on appelle fact(n) par recurrence qui termine apres n appels recursifs. Finallement fact(n+1) termine après (n+1) appels recursifs.
correction: par recurrence fact(n) = n ! :
pour n = 0 : fact(n) = fact(0) = 1 = 0! (OK)
si vrai pour n, alors $fact(n+1) = (n+1)*fact(n)$ et par hyp H.R., $fact(n) = n!$ donc $(n+1)*n! = (n+1)!$ (OK)
Complexité
Calcul de la complexité : Soit T(n) le nombre d’opérations fondamentales. Pour une fonction récurrente, c’est le nombre de résolution de la fonction de récurence. On a T(n) = T(n-1) + 1 donc T(n) = n
Analyser un algorithme récursif
Preuve de correction d’un algorithme récursif
Alan Turing (1912 – 1954) énonce ainsi son principe d’indéciablité de la terminaison d’un algorithme(1936): L’indecidabilite c’est l’impossibilité absolue et définitivement démontrée de résoudre par un procédé général de calcul un problème donné.
La terminaison, ainsi que la correction ou la complexité doivent être prouvées par des arguments mathématiques.
- terminaison : recherche du convergent
- correction / validité : recherche de l’invariant de boucle pour démontrer sa variation selon un argument de recurence
- puis finir en montrant que l’invariant de boucle ou bien le resultat obtenu repond bien à la specification de l’algorithme
Complexité d’un algorithme recursif
Pour un algorithme récursif, on compte le nombre d’appel récursif et il suffit en général de se ramener à une relation définissant une suite récurente. On se ramène souvent à évaluer une relation du type :
$$T_n = a \times T_{f(n)} + T$$
où :
- $T_n$ est la complexité pour une donnée de taille n ; a est le nombre d’appel récursif ;
- f(n) décrit la variation de n dans l’appel récursif;
- T est la complexité des calculs hors appel récursif.
| relation de récurrence sur T | solution | comportement asymtotique |
|---|---|---|
| T(n) = T(n-1) + b | T(n) = T(0) + b×n (somme de termes constants) | O(n) |
| T(n) = a×T(n-1) + b, a ≠ 1 | $T(n) = a^n × (T(0) – b/(1-a)) + b/(1-a)$ (suite géométrique) | $O(a^n)$ |
| T(n) = T(n-1) + a×n + b | T(n) = T(0) + a×n×(n+1)/2 + n×b (suite arithmetique pour le 2e terme) | $O(n^2)$ |
| T(n) = T(n/2) + b | $T(n) = T(1) + b×log_2 (n)$ | $O(log_2 n)$ |
Application : recherche du PGCD
Problème
Etant donné deux entiers naturels n et m, calculer leur pgcd (plus grand commun diviseur)
algorithme d’Euclide
Euclide propose l’algorithme suivant:
- Calculez le reste r dans la division de a par b
- Si r est nul alors le pgcd est b
- Sinon recommencer l’étape 1 avec a = b et b = r
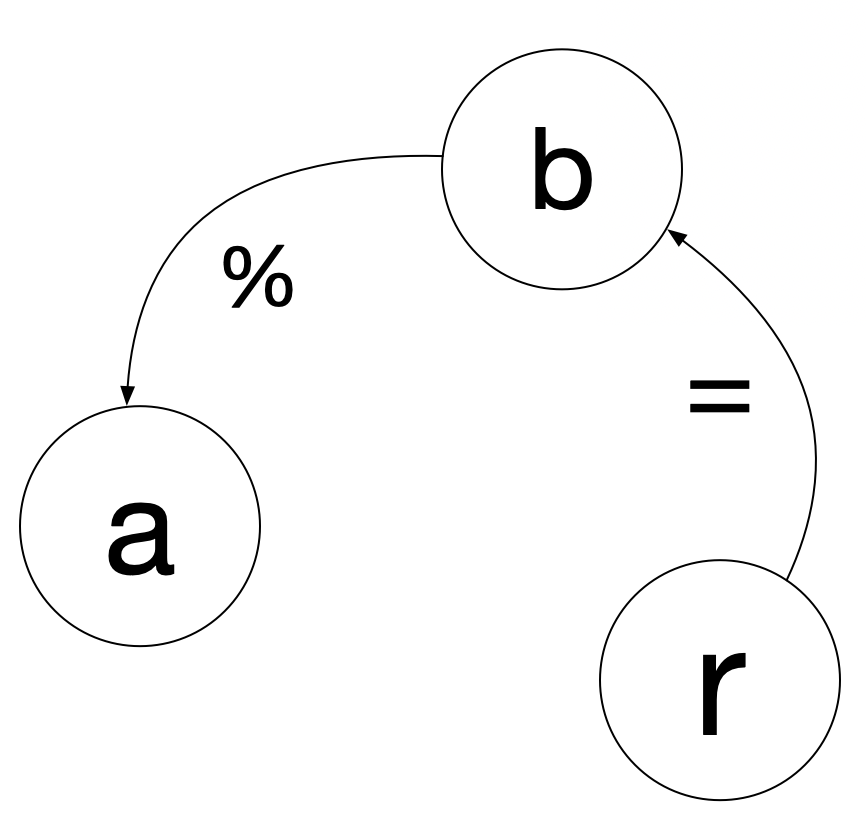
Exemple d’exécution : a = 32, b = 12 :
– 32 = (2 x 12) + 8
– 12 = (1 x 8) + 4
– 8 = (2 x 4) + 0
On a donc pgcd(32, 12) = 4
Algorithme PGCD itératif
def euclide(a,b):
"""
a et b sont des entiers, a > b
euclide retourne un entier qui est le PGCD de a et b
"""
r = a % b
while r>0 :
a = b
b = r
r = a % b
return b
algorithme recursif
def PGCD(a,b):
"""
PGCD : entier correspondant au plus grand diviseur commun de a par b
a et b : entiers tels que a > b
"""
if b == 0 : return a
else:
r = a % b
return PGCD(b,r)
Application : suite de Fibonacci
Définitions
Fibonacci était le surnom de Léonard de Pise (1170 -1250) . Il a posé un problème dans lequel il cherche à calculer le nombre de couples de lapins au bout de n années, lorsqu’ils se reproduisent selon les règles suivantes :
- Lors de la première année, l’éleveur démarre avec un couple de lapins nouveaux nés.
- Un couple de lapins donne naissance à un nouveau couple tous les ans, à partir de la 2ème année (la 1ère année, il est trop jeune).
On peut compléter le tableau suivant présentant l’effectif de ces couples de lapins :
| numero de l’année | nombre de couples de l’année précédente | nouveau nombre de couples |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 1 | 1 + 0 = 1 |
| 3 | 1 | 1 + 1 = 2 |
| 4 | 2 | 2 + 1 = 3 |
| 5 | 3 | 3 + 2 = 5 |
| 6 | … | … |

On définit la suite ($f_n$) des nombres de Fibonacci par : $$\left\{\begin{matrix}\begin{align}f_0 & =0\\f_1 & =1\\f_{n+1} & =f_{n}+f_{n-1}, \forall n \in \mathbb{N}^+\end{align}\end{matrix}\right.$$
Les nombres de Fibonacci apparaissent aussi dans la croissance des plantes. Le nombre de pétales des différentes fleurs est souvent un nombre de la suite de Fibonacci. On remarque que l’ angle entre deux primordia successifs, tend vers L’ANGLE D’OR, et que plus les nombres successifs sont grands, plus le rapport s’approche du NOMBRE D’OR.
Algorithme itératif
def fibonacci(n) :
"""
fonction qui prend en paramètre n, entier sup ou egal à O.
cette fonction utilise une variable f de type tableau.
A la fin, cette fonction retourne f[n], le terme de rang n du
tableau f qui contient les éléments entiers calculés selon l'algorithme
de fibonacci où l'élement de rang i est la somme des elements i-1 et i-2.
"""
f = []
f.append(0)
f.append(1)
if n<2:return f[n]
for i in range (2,n+1):
f.append(f[i-1] + f[i-2])
return f[n]
Exercice : Ecrire un programme qui permet d’afficher tous les nombres de la suite de Fibonacci, du rang 0 au rang n=10.
Algorithme récursif
def fibo(n):
"""
algo recursif
"""
if (n==0) : return 0
if (n==1) : return 1
return fibonacci(n-1) + fibonacci(n-2)
Parfois, l’algorithme récursif n’est pas le plus performant: Pour l’exemple de la suite de Fibonacci, on constate que les mêmes calculs sont répétés plusieurs fois, comme fibo(2) dans le cas présent pour N = 4):
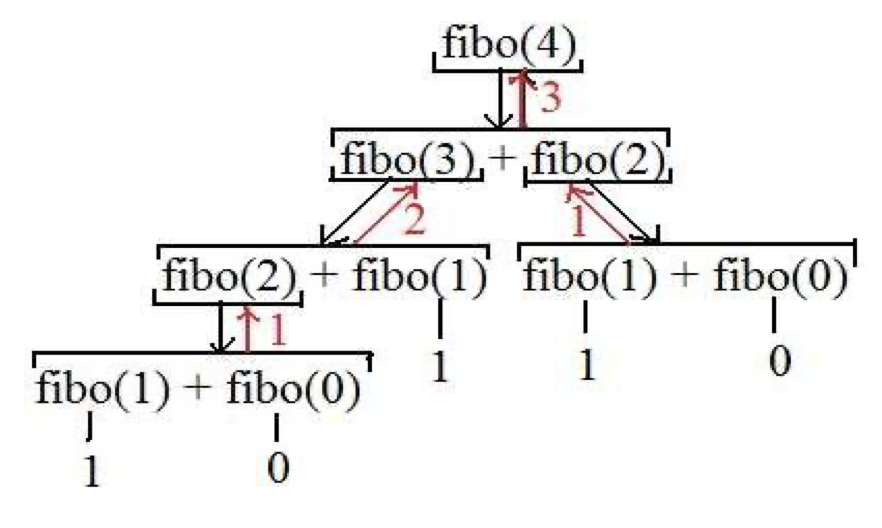
pile d'appels pour la suite de fibonacci recursive
Suite du cours
Aller à la page 2 du cours.
La récursivité intervient aussi dans de nombreux problèmes où elle s’impose comme la méthode la plus adaptée, pour ne pas dire la seule. Un exemple historique est celui des tours de Hanoi. Un jeu inventé par Edouard Lucas, vers 1880. Son traitement sur ordinateur a fait sensation, grâce à la simplicité de son script récursif…
Exercices
Ex 1 : longueur d’une liste
algorithme itératif :
def len_iterative(seq):
"""
Return the length of a list (iterative)
"""
count = 0
for elt in seq:
count = count + 1
return count
réaliser la preuve de cet algorithme.
algorithme récursif
Ecrire le script python de l’algorithme récursif
Aide pour l’écriture de l’algorithme recursif : la fonction récursive s’appelera len_recursive, et aura aussi pour argument seq. Si on veut passer en argument la liste seq de laquelle on retire le premier élément, on fait : len_recursive(seq[1:]). Il faudra alors s’inspirer de la relation de récurence suivante : $$u_{n+1} = 1 + u_n$$ lors de l’appel recursif.
Ex 2 : Exponentiation
Etudions l’exponentiation à travers deux exemples.
def exp1(n,x) :
"""
programme qui donne x^n en sortie sans utiliser **
n : entier
x : reel
exp1 : reel
"""
acc=1
for i in range(1,n+1):
acc*=x
return acc
def exp2(n,x):
"""
n : entier
x : reel
exp2 : reel
"""
if n==0 : return 1
else : return exp2(n-1,x)*x
- Combien de produits sont necessaires pour calculer une puissance n-ième avec la fonction
exp1? - Pour la fonction
exp2: Soit $u_n$ le nombre de produits nécessaires pour calculer une puissance n-ième. Quelle est la relation de récurrence vérifiée par $u_{n+1}$ ? $$u_{n+1} = u_n + …$$ - En déduire la complexité pour chacune de ces 2 fonctions.
Ex 3: dichotomie recursif
la méthode de dichotomie pour calculer la racine d’une fonction. Soit une fonction f : R → R continue, dont on sait qu’elle a une racine et une seule sur un intervalle [a, b]. On cherche une valeur approchée de cette racine. voir figure ci-dessous
principe de la dichotomie
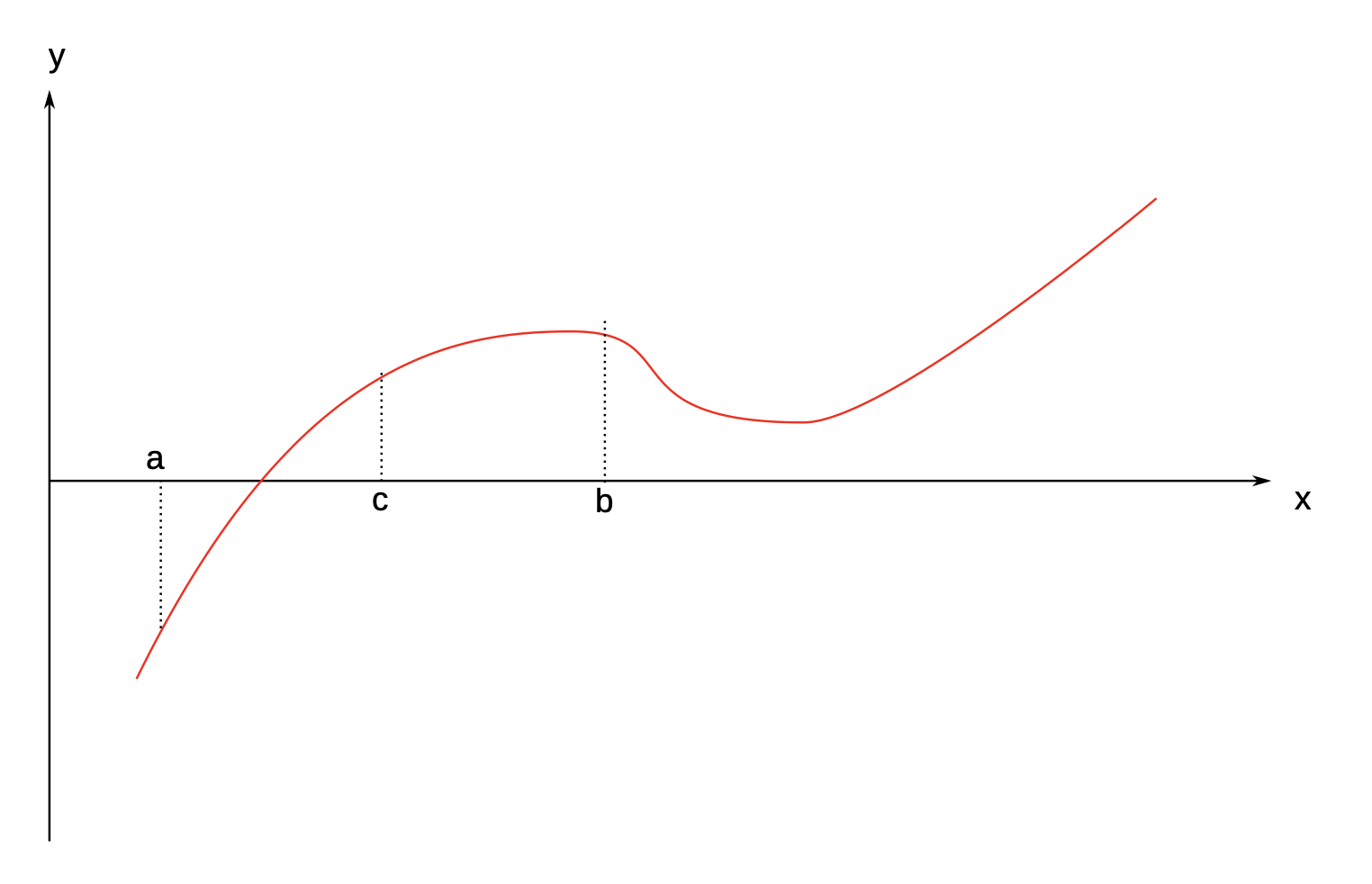
f(c) et on compare son signe à f(a) et f(b). La racine est nécessairement dans le sous-intervalle aux bornes duquel la fonction f prend deux valeurs de signes opposés (ou éventuellement nulles toutes les deux). On est donc conduit à répéter la recherche sur l’intervalle [a, c], qui est similaire au premier, d’où le caractère récursif de cet algorithme. La récursion doit être stoppée lorsque la valeur |f (c)| est inférieure à une tolérance ε que l’on fixe en fonction de la précision souhaitée.
def dichotomie_recursive(fonction,a,b,epsilon):
c = (a+b)*0.5
fc = fonction(c)
if abs(fc) < epsilon:
return c
else:
if fc*fonction(a) <= 0:
return dichotomie_recursive(fonction,a,c,epsilon)
else:
return dichotomie_recursive(fonction,c,b,epsilon)
On utilise la fonction dichotomie_recursive pour la fonction f(x):
def f(x):
return x**2-2.0
On fait alors:
> dichotomie_recursive(f,0.0,2.0,1e-3))
1.4140625
- Interpreter le résultat obtenu.
- Que valent chacun des paramètres de la fonction lors du premier appel avec
dichotomie_recursive(f,0.0,2.0,1e-3))? - Que valent chacun des paramètres lors du premier appel recursif par cette fonction?
- A quel moment cette fonction va-t-elle finir?
- Prouver la terminaison de cette fonction.
- Soit un tableau contenant des nombres entiers triés par ordre croissant :
import numpy.random
import numpy
N = 50
L = numpy.random.randint(0,200,N)
L = numpy.sort(L)
Écrire une fonction qui permet d’insérer un nombre entier x dans cette liste. La recherche de l’emplacement d’insertion doit se faire par dichotomie. Pour faire l’insertion juste avant l’élément d’indice i :
L1 = numpy.insert(L,i,x)
Cela renvoie un nouveau tableau avec l’élément inséré.
Autres exercices avec editeur online
Lien vers la page des exercices
Liens
- article sur les tours de Hanoi http://accromath.uqam.ca/2016/02/les-tours-de-hanoi-et-la-base-trois/
- algorithmes recursifs : https://fr.wikipedia.org/wiki/Algorithme_récursif
- calcul de complexité de Fibonacci recursif et programmation dynamique: univ-mlv.fr
