Dans cette deuxieme partie du cours sur la recursivité, nous allons étudier plus en detail la manière de definir la partie héredité d’un problème.
La question à laquelle on cherchera à repondre:
- supposons que le problème est/sera résolu pour le rang (n-1), comment utiliser le resultat du rang (n-1) pour resoudre le rang n?
Application de la recursivité: les tours de Hanoï
Principe
On considère trois tiges plantées dans une base. Au départ, sur la première tige sont enfilées N disques de plus en plus étroits. Le but du jeu est de transférer les N disques sur la troisième tige en conservant la configuration initiale.
On ne peut déplacer qu’un seul disque à la fois et il est interdit de poser un disque sur un autre plus petit.
il faut à un moment ou à un autre faire la place pour pouvoir déplacer le gros disque du dessous, ce qui impose d’avoir déplacé préalablement les N–1 plus petits sur un seul et même piquet, c’est-à-dire, d’avoir résolu préalablement le problème des tours de Hanoï pour ces N–1 disques :
video - resolution itérative des tours de Hanoi

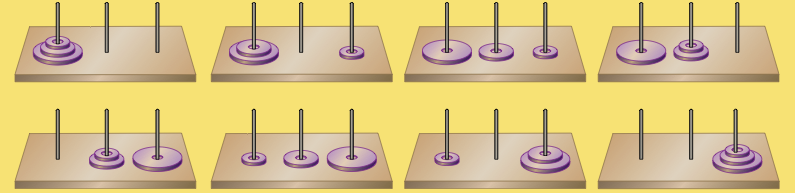
image issue du site : accromath
algorithme récursif
L’algorithme récursif pour ce problème est étonnament réduit :
def hanoi(N,d,i,a):
"""N disques doivent être déplacés de d vers a
Params:
N : int
nombre de disques
d: int
depart (vaut 1 au debut)
i: int
intermediaire (vaut 2 au debut)
a: int
fin (vaut 3 au debut)
Exemple:
lancer avec
>>> hanoi(3,1,2,3)
"""
if N==1 :
print('deplacement de {} vers {}'.format(d,a))
else:
hanoi(N-1,d,a,i)
hanoi(1,d,i,a)
hanoi(N-1,i,d,a)
Résultat
>>> hanoi(3,1,2,3)
deplacement de 1 vers 3
deplacement de 1 vers 2
deplacement de 3 vers 2
deplacement de 1 vers 3
deplacement de 2 vers 1
deplacement de 2 vers 3
deplacement de 1 vers 3
Algorithme recursif de permutation
Le problème des permutations
Une permutation d’objets distincts rangés dans un certain ordre correspond à un changement de l’ordre de succession de ces objets. https://fr.wikipedia.org/wiki/Permutation
Comment construire les permutations de abcd?
Il faut d’abord reserver a en première position. Puis réaliser toutes les permutations sur la chaine bcd. Comment fait-on cela? Il faut d’abord reserver b puis réaliser toutes les permutations sur la chaine cd… On voit clairement apparaitre l’aspect recursif de cet algorithme.
Soit la fonction permut qui realise ces permutations. La partie appelée Base sera:
def permut(mot):
if len(mot) == 1: return mot
L = []
# partie heredite a completer
Script de la partie héredité de la fonction permut
- au 1er appel de la fonction: il faut reserver chacune des lettres du mot comme premiere lettre. On commence par la premiere, “a”, correspondant au variant de boucle
i = 0:
for i in range(len(mot)):
- Il faut ensuite associer “a” avec TOUS les mots issus de la permutation de “bcd”. Cela peut être réalisé avec l’appel recursif:
for x in permut(mot[0:1] + mot[1 + 1:])
- Puis construire les chaines avec les mots mélangés retournés.
Arbre des appels recursifs
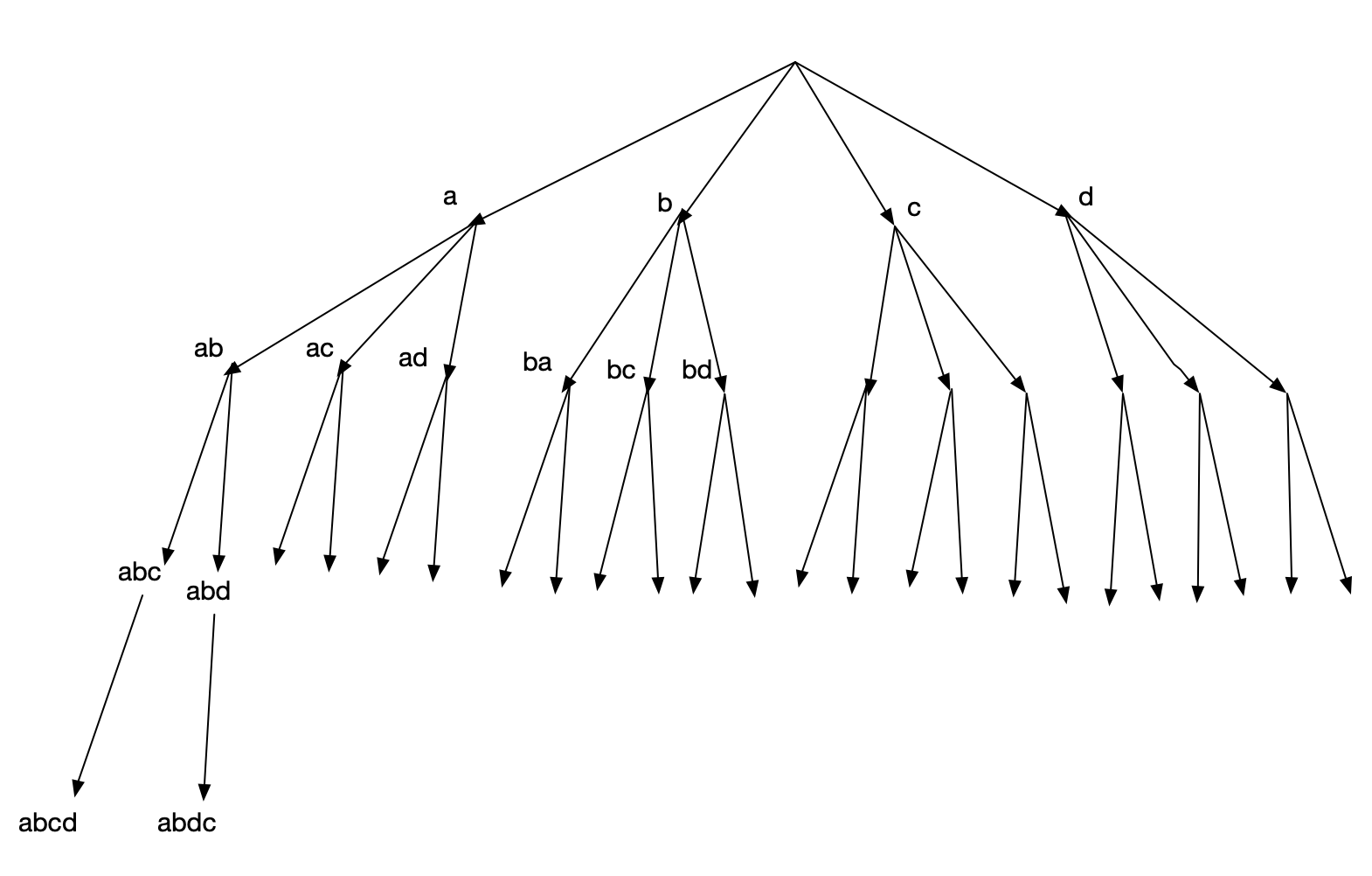
Arbre à compléter
Exercice
1. Dans un editeur Python: Compléter et tester ce script de la fonction permut avec la chaine ‘abcd’.
2. Repondre sur cahier de labo: Représenter l’arbre des appels recursifs, et compléter celui-ci.
3. cahier de labo: Quelle est la longueur de la liste retournée par cette fonction, pour ‘abcd’? Cette valeur est-elle prévisible?
4. cahier de labo: Quelle est la complexité de la fonction permut?
5. editeur Python: Créer une fonction verif qui vérifie si chaque mot permuté dans la liste est unique. Déterminer la complexité de cette nouvelle fonction. Indiquer la complexité dans le cahier de labo.
6. editeur Python: Créer une nouvelle fonction, que vous appelerez permut_noms qui donne toutes permutations de noms dans une liste. Par exemple, avec ['Riri', 'Fifi', 'Loulou'], on aura: [('Riri', 'Fifi', 'Loulou'), ('Riri', 'Loulou', 'Fifi'), ('Fifi', ...), ... ]
D’autres domaines exploitant la récursivité
La récursivité se retrouvent dans d’autres situations, où elle prend parfois d’autres noms.
L’autosimilarité
L'autosimilarité est le caractère d’un objet dans laquelle on peut trouver des similarités en l’observant à différentes échelles. Exemple : le Tapis de Sierpiński.

le Tapis de Sierpiński et l'autosimilarité
Corécursivité
Les fractales ont cette propriété d’autosimilarité, mais elles ont plutôt à voir avec un phénomène un peu différent qui s’appel la corécurisivité (ou corécursion). Le tapis de Sierpiński, du nom de Wacław Sierpiński, est une fractale obtenue à partir d’un carré. Le tapis se fabrique en découpant le carré en neuf carrés égaux avec une grille de trois par trois, et en supprimant la pièce centrale, et en appliquant cette procédure récursivement aux huit carrés restants.
Mise en abyme
La mise en abyme est un procédé consistant à représenter une œuvre dans une œuvre similaire, par exemple en incrustant dans une image cette image elle-même.

L’intrigue du film Inception
Dans «Inception», Nolan voulait explorer l’idée de personnes partageant un espace de rêve. Cela vous donne la possibilité d’accéder à l’inconscient de quelqu’un. La majorité de l’intrigue du film se déroule dans ces mondes oniriques interconnectés. Cette structure crée un cadre dans lequel les actions dans les mondes réels ou oniriques se répercutent sur les autres.

Travail pratique
Lien vers le TP: dessins recursifs
Liens
-
Approfondir : voir la page https://fr.wikipedia.org/wiki/Algorithme_récursif
-
un bon exemple de l’exercice des permutations: les menus pascal.ortiz.free.fr
-
Site de Gerard Vuillemin
