Créer et resoudre un labyrinthe
Les scripts suivants permettent de créer un labyrinthe de manière aléatoire, et d’exploiter la structure de données de ce labyrinthe. On pourra ainsi tester quelques algorithmes relatifs au parcours de ce labyrinthe. Les scripts en permettent une visualisation.
Définitions des classes
class Pile:
def __init__(self):
self.lst = []
def empty(self):
return self.lst == []
def push(self, x):
self.lst.append(x)
def pop(self):
if self.empty():
raise ValueError("pile vide")
return self.lst.pop()
def explorer(laby):
pile = Pile()
pile.push((0, laby.q - 1))
laby.tab[0][laby.q - 1].etat = False
while True:
i, j = pile.pop()
if i == laby.p - 1 and j == 0:
break
if j > 0 and laby.tab[i][j].S and laby.tab[i][j-1].etat:
pile.push((i, j))
pile.push((i, j-1))
laby.tab[i][j-1].etat = False
elif i < laby.p-1 and laby.tab[i][j].E and laby.tab[i+1][j].etat:
pile.push((i, j))
pile.push((i+1, j))
laby.tab[i+1][j].etat = False
elif j < laby.q-1 and laby.tab[i][j].N and laby.tab[i][j+1].etat:
pile.push((i, j))
pile.push((i, j+1))
laby.tab[i][j+1].etat = False
elif i > 0 and laby.tab[i][j].W and laby.tab[i-1][j].etat:
pile.push((i, j))
pile.push((i-1, j))
laby.tab[i-1][j].etat = False
return pile.lst
class Case:
def __init__(self):
self.N = False
self.W = False
self.S = False
self.E = False
self.etat = False
class Labyrinthe:
def __init__(self, p, q):
self.p = p
self.q = q
self.tab = [[Case() for j in range(q)] for i in range(p)]
def show(self):
plt.plot([0, 0, self.p, self.p, 0], [0, self.q, self.q, 0, 0], linewidth=2)
for i in range(self.p-1):
for j in range(self.q):
if not self.tab[i][j].E:
plt.plot([i+1, i+1], [j, j+1], 'b')
for j in range(self.q-1):
for i in range(self.p):
if not self.tab[i][j].N:
plt.plot([i, i+1], [j+1, j+1], 'b')
plt.axis([-1, self.p+1, -1, self.q+1])
plt.show()
def solution(self):
sol = explorer(self)
X, Y = [], []
for (i, j) in sol:
X.append(i+.5)
Y.append(j+.5)
X.append(self.p-.5)
Y.append(.5)
plt.plot(X, Y, 'r', linewidth=2)
self.show()
def creation(p, q):
laby = Labyrinthe(p, q)
pile = Pile()
i, j = randint(p), randint(q)
pile.push((i, j))
laby.tab[i][j].etat = True
while not pile.empty():
i, j = pile.pop()
v = []
if j < q-1 and not laby.tab[i][j+1].etat:
v.append('N')
if i > 0 and not laby.tab[i-1][j].etat:
v.append('W')
if j > 0 and not laby.tab[i][j-1].etat:
v.append('S')
if i < p-1 and not laby.tab[i+1][j].etat:
v.append('E')
if len(v) > 1:
pile.push((i, j))
if len(v) > 0:
c = v[randint(len(v))]
if c == 'N':
laby.tab[i][j].N = True
laby.tab[i][j+1].S = True
laby.tab[i][j+1].etat = True
pile.push((i, j+1))
elif c == 'W':
laby.tab[i][j].W = True
laby.tab[i-1][j].E = True
laby.tab[i-1][j].etat = True
pile.push((i-1, j))
elif c == 'S':
laby.tab[i][j].S = True
laby.tab[i][j-1].N = True
laby.tab[i][j-1].etat = True
pile.push((i, j-1))
else:
laby.tab[i][j].E = True
laby.tab[i+1][j].W = True
laby.tab[i+1][j].etat = True
pile.push((i+1, j))
return laby
Librairies
from numpy.random import randint
import matplotlib.pyplot as plt
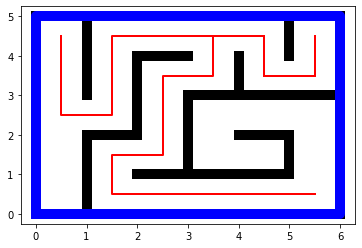
Un premier exemple
laby = creation(6, 5)
laby.solution()
Exploration de la structure de données
def directions(laby,i,j):
"""les directions possibles pour la case courante
i : int numero de ligne
j : numero de la colonne
retourne une liste (tuple) des points cardinaux possibles
"""
L = []
if laby.tab[j][i].N == True: L.append('N')
if laby.tab[j][i].S == True: L.append('S')
if laby.tab[j][i].E == True: L.append('E')
if laby.tab[j][i].W == True: L.append('W')
return tuple(L)
Un labyrinthe est un tableau de cases laby.tab[j][i] ayant chacune pour propriétés : N,S,E,W
- i : int numero de ligne
- j : numero de la colonne
Pour chacune de ces propriétés, par exemple laby.tab[j][i].Non renseigne une valeur True ou False
- True : direction possible
- False : impossible (mur)
Créer un labyrinthe vide
def labyrinthe(lines,col):
"""
Params :
--------
lines : int : nombre de lignes du labyrinthe
col : int : nombre de colonnes
Returns :
---------
tab2 : list : tuples de 1 à 4 éléments correspondants aux directions libres ('N', 'S', E', 'W')
sortie : tracé du labyrinthe
Variables :
-----------
p : nombre de colonnes (=largeur)
q : nombre de lignes (=hauteur)
"""
laby = creation(col, lines)
tab2 = [[0]*laby.p for i in range(laby.q)]
for i in range(laby.q):
for j in range(laby.p):
tab2[i][j] = directions(laby,i,j)
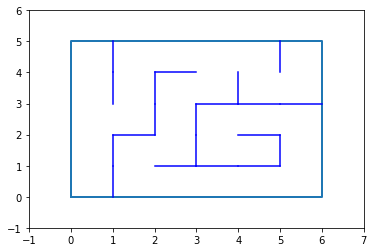
Labyrinthe.show(laby)
return tab2
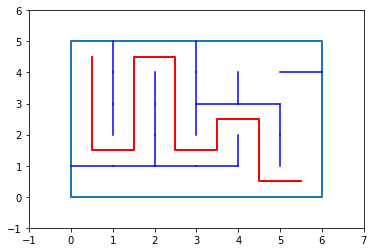
tab=labyrinthe(5,6)
tab
[[('N',), ('N', 'E'), ('E', 'W'), ('E', 'W'), ('E', 'W'), ('N', 'W')],
[('N', 'S'), ('S', 'E'), ('N', 'W'), ('N', 'E'), ('W',), ('N', 'S')],
[('N', 'S', 'E'), ('N', 'W'), ('N', 'S'), ('S', 'E'), ('E', 'W'), ('S', 'W')],
[('N', 'S'), ('N', 'S'), ('S', 'E'), ('N', 'W'), ('N', 'E'), ('N', 'W')],
[('S',), ('S', 'E'), ('E', 'W'), ('S', 'E', 'W'), ('S', 'W'), ('S',)]]
Remarque : Les lignes sont mises dans l’ordre inverse du dessin du labyrinthe :
Tracé du labyrinthe
def mur(dir,i,j):
"""trace les murs des directions fermées
dir est un tuple contenant les directions libres
"""
line = 10
if not('N' in dir[i][j]) : plt.plot([j,j+1],[i+1,i+1],'black',linewidth=line)
if not('S' in dir[i][j]) : plt.plot([j,j+1],[i,i],'black',linewidth=line)
if not('E' in dir[i][j]) : plt.plot([j+1,j+1],[i,i+1],'black',linewidth=line)
if not('W' in dir[i][j]) : plt.plot([j,j],[i,i+1],'black',linewidth=line)
def murs(tab):
for i in range(len(tab)):
for j in range(len(tab[i])):
mur(tab,i,j)
plt.plot([0, 0, len(tab[0]), len(tab[0]), 0], [0, len(tab), len(tab), 0, 0], 'blue',linewidth=10)
plt.savefig('labyrinthe.png')
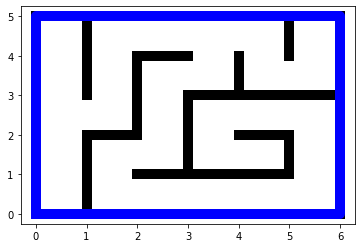
On peut faire l’économie du tracé eventuel côté S et côté W grace au tracé des cases adjacentes.
murs(tab)
Parcours du labyrinthe
fonctions utiles
def nexto(c,direc):
"""retourne les coordonnées lors du deplacement
selon la position actuelle et la direction
Params :
--------
c : tuple (ligne,colonne) correspondant à (y,x) dans le plan cartesien
direct : str : 'N', 'S', E', 'W'
Returns :
---------
tuple : (int,int) correspondant à (ligne,colonne)
"""
i,j = c[0],c[1]
if direc=='N' : return (i+1,j)
if direc=='S' : return (i-1,j)
if direc=='E' : return (i,j+1)
if direc=='W' : return (i,j-1)
def visited(c,L,couleur):
"""retourne la couleur du noeud de coord c et
de liste de directions possibles L selon celle de ses voisins
Params :
--------
c : tuple : (ligne,colonne) correspondant à (y,x) dans le plan cartesien
L : list : tuples de 1 à 4 éléments correspondants aux directions libres ('N', 'S', E', 'W')
couleur : List dimension 2 contenant des elements str
'white' si noeud non visité,
'green' si le noeud est en cours de visite,
'red' si tous les noeuds ont été visités autour de lui
Returns :
---------
couleur : str : 'green' si le noeud est en cours de visite, 'red' si tous les noeuds
ont été visités autour de lui
"""
i,j = c[0],c[1]
coul='red'
for direc in L:
coord = nexto(c,direc)
if couleur[coord[0]][coord[1]]=='white':coul='green'
print(c,coul)
return coul
une premiere idée : colorer les noeuds du chemin en vert
def trouvercheminiter(start,end,tab):
"""recherche du chemin jusqu'à la sortie dans le labyrinthe
en utilisant une technique qui s'apparente au parcours en profondeur
avec backtracking
on utilise une pile de noeuds visités
Params :
--------
start : tuple de coord dans le labyrinthe
end : tuple de coord dans le labyrinthe
tab : liste de liste contenant pour chaque tuple de coordonnées un tuple de directions possibles
Variables :
-----------
couleur : une table de la couleur du noeud ('red' si aucune nouvelle direction possible,
'green' si en cours de visite, 'white' si jamais visité)
Returns:
--------
la liste couleur
"""
p = Pile()
p.push(start)
c = start
couleur = [['white']*len(tab[0]) for i in range(len(tab))]
# precaution pour eviter debordement
compt = 0
while (not p.empty()) and (not c == end) and compt<100:
compt+=1
c = p.pop()
L = tab[c[0]][c[1]]
couleur[c[0]][c[1]]=visited(c,L,couleur) # c est retiré de la pile et coloré en green ou red
for direc in L:
coord = nexto(c,direc)
if couleur[coord[0]][coord[1]]=='white': # le noeud fils est coloré en blanc dans la direction D
for n in tab[coord[0]][coord[1]]:
p.push(coord)
# alors on ajoute le noeud fils dans la direction D au sommet de la pile
# n fois afin de reconsidérer sa couleur à chaque fois que l'on depile
return couleur
trouvercheminiter((len(tab)-1,0),(0,len(tab[0])-1),tab)
(4, 0) green
(3, 0) green
(2, 0) green
(2, 1) green
(3, 1) green
(4, 1) green
(4, 2) green
(4, 3) green
(4, 4) green
(3, 4) green
(3, 5) green
(4, 5) red
(3, 5) red
(3, 4) red
(4, 4) red
(3, 3) green
(3, 2) green
(2, 2) green
(1, 2) green
(1, 1) green
(0, 1) green
(0, 2) green
(0, 3) green
(0, 4) green
(0, 5) green
[['white', 'green', 'green', 'green', 'green', 'green'],
['white', 'green', 'green', 'white', 'white', 'white'],
['green', 'green', 'green', 'white', 'white', 'white'],
['green', 'green', 'green', 'green', 'red', 'red'],
['green', 'green', 'green', 'green', 'red', 'red']]
Une autre approche : mémoriser les étapes de la solution
def solution(start,end,tab):
"""trouve la solution au labyrinthe et trace ce chemin
La recherche du chemin jusqu'à la sortie dans le labyrinthe
utilise une technique qui s'apparente au parcours en profondeur
avec backtracking
on utilise une pile de noeuds visités
Params :
--------
start : tuple de coord dans le labyrinthe
end : tuple de coord dans le labyrinthe
tab : liste de liste contenant pour chaque tuple de coordonnées un tuple de directions possibles
Returns:
--------
la liste couleur
Variables :
-----------
couleur : une table de la couleur du noeud ('red' si aucune nouvelle direction possible,
'green' si en cours de visite, 'white' si jamais visité)
p : Pile() utile pour la recherche du parcours
pchemin : Pile() utile pour memoriser ce chemin
"""
p = Pile()
pchemin = Pile()
p.push(start)
c = start
couleur = [['white']*len(tab[0]) for i in range(len(tab))]
while (not p.empty()) and (not c == end):
c = p.pop()
pchemin.push(c)
L = tab[c[0]][c[1]]
couleur[c[0]][c[1]]=visited(c,L,couleur) # c est retiré de la pile et coloré en green ou red
noeud = pchemin.pop()
while couleur[noeud[0]][noeud[1]] == 'red':
noeud = pchemin.pop() # il peut y avoir plusieurs fois le noeud successivement dans la pile
pchemin.push(noeud) # on remet le dernier noeud retiré non rouge
for direc in L:
coord = nexto(c,direc)
if couleur[coord[0]][coord[1]]=='white': # le noeud fils est coloré en blanc dans la direction D
#for n in tab[coord[0]][coord[1]]:
p.push(c)
p.push(coord)
# alors on ajoute le noeud fils dans la direction D au sommet de la pile
# ainsi que son noeud parent
return pchemin.lst
def murSolution(tab,L):
xList=[]
yList=[]
for i in range(len(tab)):
for j in range(len(tab[i])):
mur(tab,i,j)
plt.plot([0, 0, len(tab[0]), len(tab[0]), 0], [0, len(tab), len(tab), 0, 0], 'blue',linewidth=10)
for n in range(len(L)):
yList.append(L[n][0]+0.5)
xList.append(L[n][1]+0.5)
plt.plot(xList,yList,'red',linewidth=2)
L= solution((len(tab)-1,0),(0,len(tab[0])-1),tab)
L
(4, 0) green
(3, 0) green
(2, 0) green
(2, 1) green
(3, 1) green
(4, 1) green
(4, 2) green
(4, 3) green
(4, 4) green
(3, 4) green
(3, 5) green
(4, 5) red
(3, 5) red
(3, 4) red
(4, 4) red
(4, 3) green
(3, 3) green
(3, 2) green
(2, 2) green
(1, 2) green
(1, 1) green
(0, 1) green
(0, 2) green
(0, 3) green
(0, 4) green
(0, 5) green
[(4, 0),
(3, 0),
(2, 0),
(2, 1),
(3, 1),
(4, 1),
(4, 2),
(4, 3),
(4, 3),
(3, 3),
(3, 2),
(2, 2),
(1, 2),
(1, 1),
(0, 1),
(0, 2),
(0, 3),
(0, 4),
(0, 5)]
murSolution(tab,L)
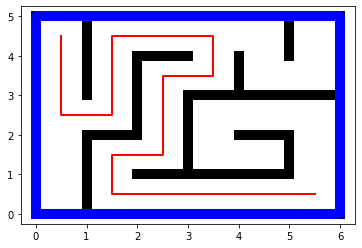
mémoriser TOUTES les étapes du parcours
def parcours(start,end,tab):
"""trouve la solution au labyrinthe et trace ce chemin
p : Pile() utile pour la recherche du parcours
pchemin : Pile() utile pour memoriser tout le chemin
on insère dans le chemin toutes les arêtes empruntées :
pour le chemin entre c1 et c2, on insère c1 puis c2
"""
p = Pile()
pchemin = Pile()
p.push(start)
c = start
couleur = [['white']*len(tab[0]) for i in range(len(tab))]
while (not p.empty()) and (not c == end):
c = p.pop()
pchemin.push(c) # chaque fois que l'on depile, on rempile dans pchemin
L = tab[c[0]][c[1]]
couleur[c[0]][c[1]]=visited(c,L,couleur) # c est retiré de la pile et coloré en green ou red
for direc in L:
coord = nexto(c,direc)
if couleur[coord[0]][coord[1]]=='white': # le noeud fils est coloré en blanc dans la direction D
p.push(c) # on remet le noeud parent afin de reconsidérer sa couleur à chaque fois que l'on depile
# et le chemin arriere CONTINU pour le tracé
p.push(coord)
# alors on ajoute le noeud fils dans la direction D au sommet de la pile
return pchemin.lst
L = parcours((len(tab)-1,0),(0,len(tab[0])-1),tab)
L
(4, 0) green
(3, 0) green
(2, 0) green
(2, 1) green
(3, 1) green
(4, 1) green
(4, 2) green
(4, 3) green
(4, 4) green
(3, 4) green
(3, 5) green
(4, 5) red
(3, 5) red
(3, 4) red
(4, 4) red
(4, 3) green
(3, 3) green
(3, 2) green
(2, 2) green
(1, 2) green
(1, 1) green
(0, 1) green
(0, 2) green
(0, 3) green
(0, 4) green
(0, 5) green
[(4, 0),
(3, 0),
(2, 0),
(2, 1),
(3, 1),
(4, 1),
(4, 2),
(4, 3),
(4, 4),
(3, 4),
(3, 5),
(4, 5),
(3, 5),
(3, 4),
(4, 4),
(4, 3),
(3, 3),
(3, 2),
(2, 2),
(1, 2),
(1, 1),
(0, 1),
(0, 2),
(0, 3),
(0, 4),
(0, 5)]
murSolution(tab,L)