Graphe pondéré : Algorithme de Dijkstra
On va voir une variante, plus complexe, de l’algorithme BFS : l’algorithme de Dijkstra. Cet algorithme permettra de calculer toutes les distances entre un sommet de départ r et les autres sommets, mais cette fois ci, ce graphe est pondéré.
Pour un graphe pondéré, chaque arête (u,v) a une longueur notée l(u,v). Pour certaines applications, on parle plutôt de poids d’une arête. Jusqu’à présent nous n’avons traité que le cas particulier où l(u,v) = 1.
Comme l’algorithme précédent, celui-ci donnera la distance selon le plus court chemin.
Au départ, aucune distance n’est connue. Les distances provisoires notées distG(r,u), sont mises à l’infini : pour tout u, distG(r,u) = ∞
Le graphe suivant servira d’exemple :
exemple de graphe pondéré
La méthode employée diffère légèrement de celle du parcours en largeur. Il faudra également utiliser une liste L de sommet à parcourir. Mais cette liste est constament remise à jour (triée) en fonction des longueurs des arêtes constatées, comme on le verra plus loin.
De plus, il faudra mémoriser le sommet parent d’un sommet visité. Ce sommet parent pourra être modifié si on trouve un chemin plus court pour atteindre ce sommet depuis le sommet de départ.
algorithme
On part du sommet r :
- On visite tous les noeuds fils de
r. Pour chaque sommet adjacentu: On note la distance qui séparerdeuselon la longueur de l’arête. Et on note le sommet parent. On ajoute chaque sommet dans la listeL. - On trie la liste
Lpar ordre de distance àrcroissante. - On colore en rouge le sommet
rlorsque tous les sommets adjacents ont été visités. Et on retirerde la liste. - On passe au sommet
vpour poursuivre l’exploration : le premier à gauche dans la liste (celui le plus proche der). - On visite tous les sommets voisins de
v. On les ajoute dans la liste L. - Pour chaque voisin
wdu sommetv: si distG(r,w) < distG(r,v) + distG(v,w), c’est que le sommetwa déjà été visité, et que le chemin déjà trouvé est plus court que le chemin actuel. On ne fait rien. - si distG(r,w) > distG(r,v) + distG(v,w), c’est que le sommet
wa peut être été visité, mais que le chemin actuel est le plus court. On note alors la nouvelle valeur de la distance : distG(r,w) = distG(r,v) + distG(v,w). Et on note que le parent du sommetwestv. C’est actuellement le meilleur chemin. - Puis, lorsque tous les voisins de
vont été visités, on revient au point 2 pourv(trier la liste L, coloration en rouge,…).
Ce qui change par rapport à l’algorithme précédent, c’est surtout le nouveau choix de sommet à visiter lors du parcours du graphe : lorsque tous les noeuds fils d’un sommet ont été visités, et que l’on a mémorisé leur distance au sommet de départ, on choisi d’explorer le sommet le plus proche, celui le plus à gauche dans la liste L.
Il faut donc trier cette liste à la fin de chaque exploration.
Illustration
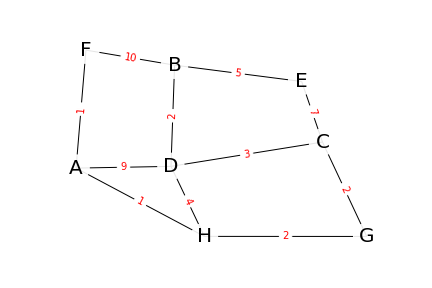
On démarre du sommet Bvoisins. Après le parcours de ses voisins, la liste L contient les sommets D,E,F classés par ordre de distance croissante :
$$L = [(D,2), (E,5), (F,10)]$$
- D est à une distance de 2
- E est à une distance de 5
- F est à une distance de 10
L = [(D,2), (E,5), (F,10)]
B:
| exploration depuis le sommet… | A | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| B | ∞ | ∞ | 2 | 5 | 10 | ∞ | ∞ |
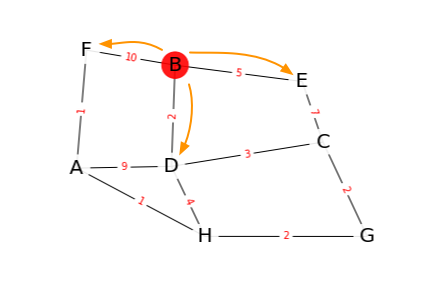
Ensuite, on passe au sommet D, le plus proche de B (le plus à gauche dans la liste) :
- C est à une distance 2+3 = 5 de B
- H est à une distance 2+4 = 6 de B
- A est à une distance 2+9 = 11 de B
On ajoute C, H et A à la liste. L = [(E,5), (F,10), (C,5), (H,6), (A,11)]
Puis on trie cette liste:
L = [(C,5), (E,5), (H,6), (F,10), (A,11)]
| exploration depuis le sommet… | A | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| D | 11 | 5 | ∞ | 6 |
Les valeurs pour D, E et F ne sont pas remises à jour. On ne les mentionne pas dans ce tableau.
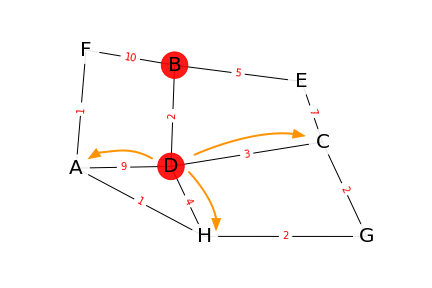
Le sommet suivant à traiter est alors le C. Ses voisins sont E, et G. L’examen du chemin vers E ne change rien : le chemin B,D,C,E a une longueur plus importante que le chemin direct B,E (12>5). Par contre, le chemin vers G offre une nouvelle distance :
- G est à une distance 5+2 = 7 de B :
| exploration depuis le sommet… | A | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| C | 7 |
On ajoute G à la liste et on trie:
L = [(E,5), (H,6), (G,7), (F,10), (A,11)]
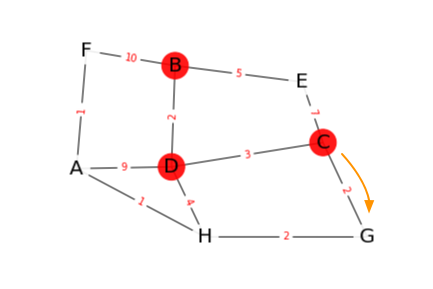
- A est à une distance 6+1 = 7 du noeud B. C’est le meilleur chemin.
- G est à une distance 6+2 = 8 du noeud B en passant par H. Cette valeur n’est pas enregistrée car il existe un chemin plus court.
| exploration depuis le sommet… | A | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| H | 7 |
L = [(A,7), (G,7), (F,10)]
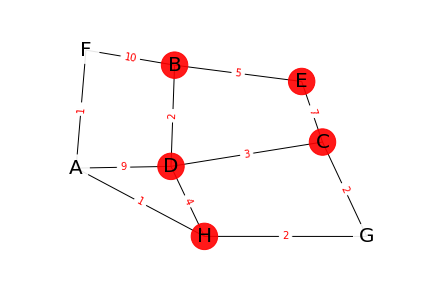
Fin de l'exploration
| exploration depuis le sommet… | A | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| A | 8 |
Ainsi, le plus court chemin pour faire B => F est trouvé en remontant dans les tableaux successifs:
- F est à une distance 8 de B en passant par A
- A est à une distance 7 de B en passant par H
- H est à une distance 6 de B en passant par D
- D est à une distance 2 de B
Arbre représentant ce graphe
L’arbre représentant les plus courts chemins est alors le suivant :
arbre couvrant
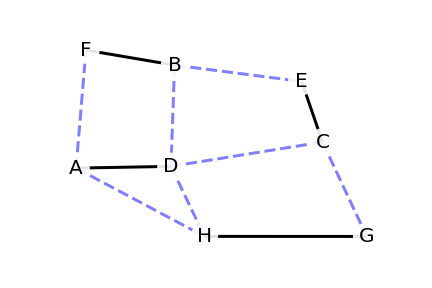
On peut le représenter avec une forme plus conventionnelle :
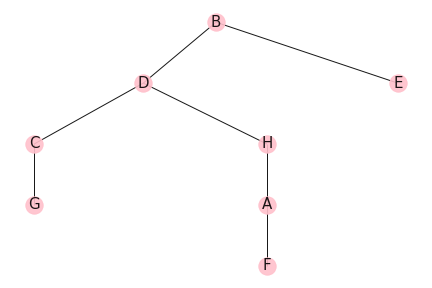
arbre de plus court chemin
