voir le notebook sur trajectoire parabolique
Animation
Sur la page du
site phet.colorado
- demarrer l’animation (clic sur l’image)
- Choisissez “Introduction”.
- Cochez les quatre cases (en haut à droite).
- Cochez aussi “Ralenti”.
Commencez par la rampe du milieu (juste une descente). Faites descendre le skateur et observez bien tout, pendant la descente puis sur la zone plate (même si vous ne voyez plus le skateur).
Comment varie la vitesse ? Comment varie l’énergie potentielle ? L’énergie cinétique ? L’énergie totale ?
Augmentez sa masse.
Qu’est-ce qui varie, qu’est-ce qui ne change pas ?
Passez ensuite à la rampe en U.
Mêmes questions. Et jusqu’à quelle hauteur remonte-t-il ?
Augmentez sa masse.
Qu’est-ce qui varie, qu’est-ce qui ne change pas ?
Puis terminez par la rampe double (mêmes questions).
Energie cinetique
Pour un système matériel de masse m et de vitesse v, l’energie cinétique Ec est:
$$Ec = \tfrac{1}{2}\times m \times v^2$$
Faire les exercices 4p268 et 5p268 du livre hachette
Travail d’une force
Le travail d’une force représente le gain d’énergie cinétique que cette force est capable d’apporter au système pendant une durée Dt.
Soit un déplacement $\overrightarrow{AB}$ et une force $\overrightarrow{F}$ appliquée au système pendant tout le deplacement :
Le travail WA->B se calcule selon l’expression :
$$W_{AB} = \overrightarrow{F}.\overrightarrow{AB} = F.AB.cos~\alpha$$
- W est en JOULES
- α est l’angle formé entre les vecteurs $\overrightarrow{AB}$ et la force $\overrightarrow{F}$
On considère 3 cas :
- α<90 : travail moteur (schémas 1 et 2 ci-dessous)
- α>90 : travail resistant (schémas 4 et 5)
- α=90 : travail nul (schéma 3)
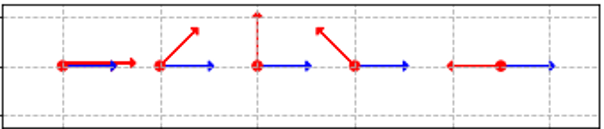
angle formé entre les vecteurs
Théorème de l’énergie
Le travail d’une force $\overrightarrow{F}$ sur un déplacement $\overrightarrow {AB}$ est responsable de la variation d’énergie cinétique entre A et B:
$$Ec(B) - Ec(A) = W_{AB} = \overrightarrow{F}.\overrightarrow{AB}$$
Energie potentielle de pesanteur d’un système
Lorsqu’un objet de masse m se situe à une hauteur h, il possède une énergie qui est susceptible de lui fournir de l’énergie cinétique.
Par exemple, une balle tenue à une hauteur de 1m, dans la main: si on ouvre la main, la balle va acquerir de la vitesse, et donc de l’énergie mécanique.
Cette énergie contenue est de l'énergie potentielle.
Il existe plusieurs définitions pour l’énergie potentielle. Celle-ci dérive d’une force d’interaction, conservative.
Pour la force de pesanteur, la définition de l’énergie potentielle est:
$$Ep(z) = m.g.z + constante$$
Souvent, la constante est prise comme égale à zero, ce qui fait Ep(z) = mgz.
Ex 12p269 (corrigé dans le livre)
Energie mecanique
Définition
L’énergie mécanique Em d’un système est la somme de son énergie cinétique Ec et de son énergie potentielle Ep.
$$Em = Ec + Ep$$
Conservation de l’énergie mécanique
Pour un système soumis à des forces conservatives (comme le poids par exemple), ou à des forces dont le travail est nul, l’énergie mécanique se conserve au cours du mouvement:
$$Em = constante$$
Soit un système dont l’énergie mécanique se conserve sur le déplacement AB:
$$Em(A) = Em(B)$$
Soit:
$$Ec(A) + Ep(A) = Ec(B) + Ep(B)$$
Non conservation de l’énergie mécanique
Lorsqu’un système est soumis à une force non conservative $\overrightarrow{F}$ sur son déplacement AB, la variation d’énergie mécanique $\Delta Em$ est égale au travail $W_{AB}(\overrightarrow{F})$ de cette force:
$$\Delta Em = Em(B) - Em(A) = W_{AB}(\overrightarrow{F})$$
Lire la page 263 du livre hachette
