- introduction aux graphes
- cours sur les graphes. Term NSI
- algorithmes de parcours des graphes
- TP sur les algorithmes de parcours des graphes
- algorithme de Dijkstra
- Protocoles de routage
- Arbres
Utiliser un outil en ligne
Pour une première approche du traitement sur un graphe: Ouvrir l’application en ligne https://graphonline.ru/fr/
Plus court chemin
Vous pourrez alors créer un premier graphe de type: sous-réseaux en étoile. Ce graphe pourrait être la représentation d’un réseau social, ou bien de 2 sous-réseaux interfacés par un routeur.
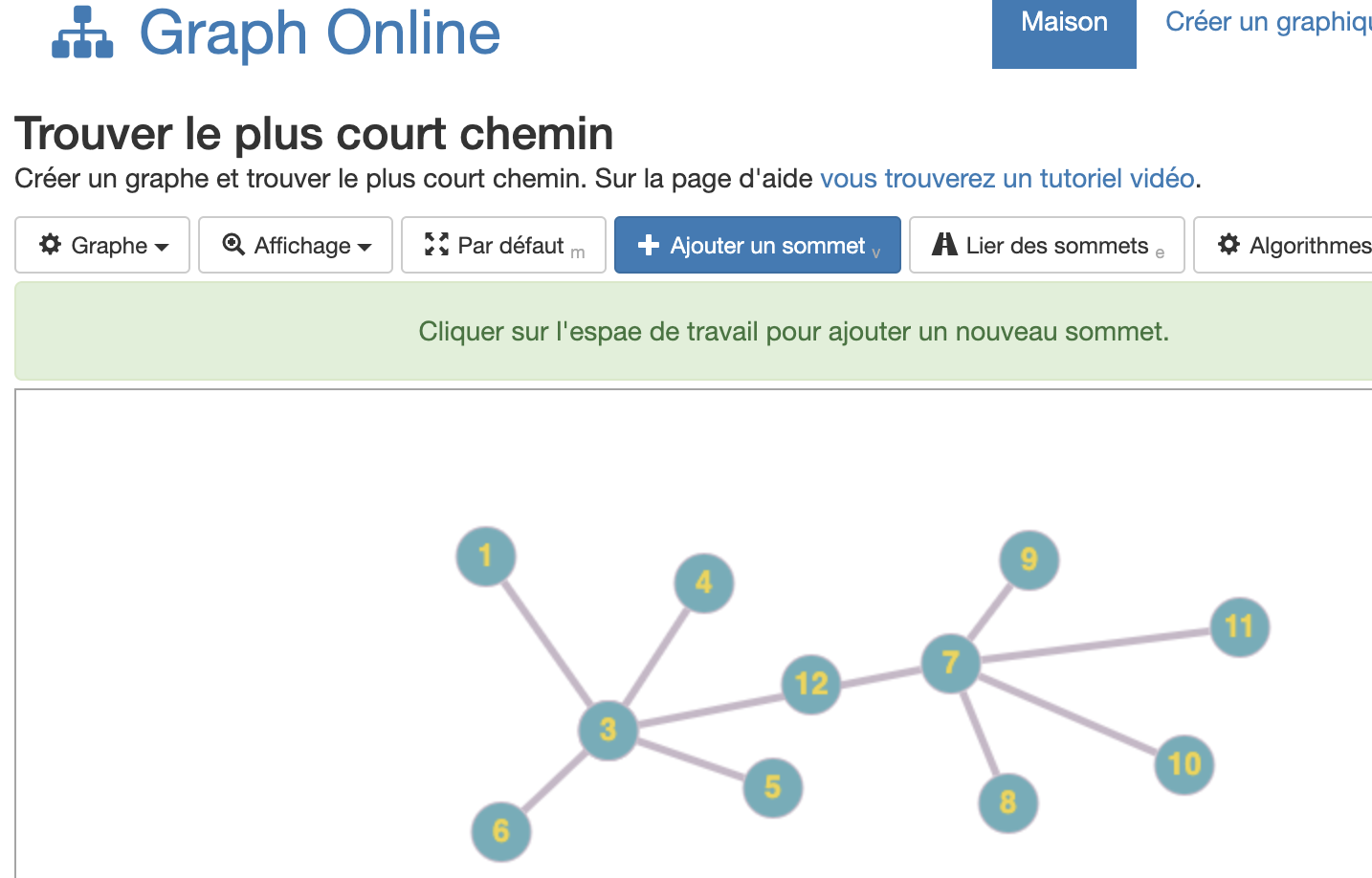
Une fois le graphe réalisé, explorer le menu des Algorithmes, et sélectionner:
- le degré des sommets
- le rayon du graphe
- l’arbre couvrant minimal
- la Recherche du plus court chemin entre 2 sommets du graphe.
Combien d’arêtes séparent les sommets les plus éloignés de ce graphe?
Chemin Eulérien
La page wikipedia présente ce qu’est un chemin eulérien.
Représenter chacun des 2 graphes suivants, l’un après l’autre, et chercher la présence (ou non) d’un chemin eulérien dans une telle figure.
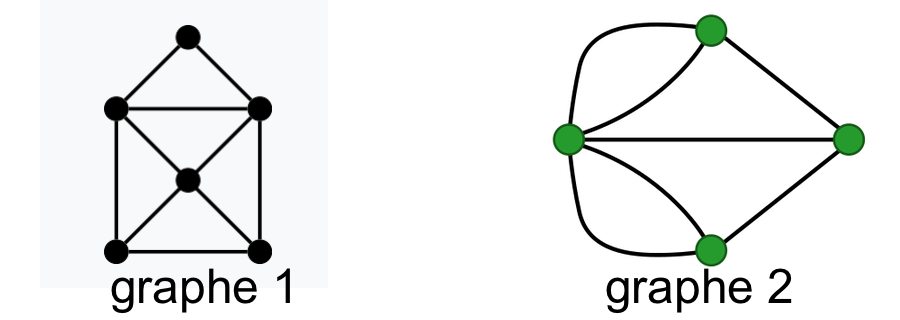
Q.a: Comment modifier (à minima) le graphe 2 pour qu’il présente un chemin eulérien?
Traitement des graphes en Python
Dessiner le graphe avec la librairie networkx
Dans un notebook python, saisir les lignes:
import matplotlib.pyplot as plt
import networkx as nx
from numpy import array
G = nx.Graph()
# definition des noeuds
G.add_node(0,label='A',col='white')
G.add_node(1,label='B',col='white')
G.add_node(2,label='C',col='white')
G.add_node(3,label='D',col='white')
# definition des aretes
G.add_edge(0,1)
G.add_edge(0,2)
G.add_edge(2,3)
Rappel:
- Anglais: Node; Français: Sommet (noeud)
- Anglais: Edge; Français: Arête
Puis, dans une nouvelle cellule, ajouter les 3 parties suivantes:
- Dessin des sommets
# calcul des positions pour repartir les sommets du graphe
pos = nx.spring_layout(G)
# dessin des sommets
L = list(G.nodes(data='col'))
colorNodes = [node[1] for node in L]
nx.draw_networkx_nodes(G, pos, node_size=700,node_color=colorNodes,alpha=0.9)
- Afficher les étiquettes
# labels
labels_nodes={node:label for node,label in G.nodes(data='label')}
nx.draw_networkx_labels(G, pos, labels=labels_nodes, \
font_size=20, \
font_color='black', \
font_family='sans-serif')
- Dessiner les arêtes
# edges
nx.draw_networkx_edges(G, pos)
plt.axis('off')
plt.show()
Q.b: Modifier maintenant la déclaration du graphe (cellule 1) pour dessiner le graphe suivant:
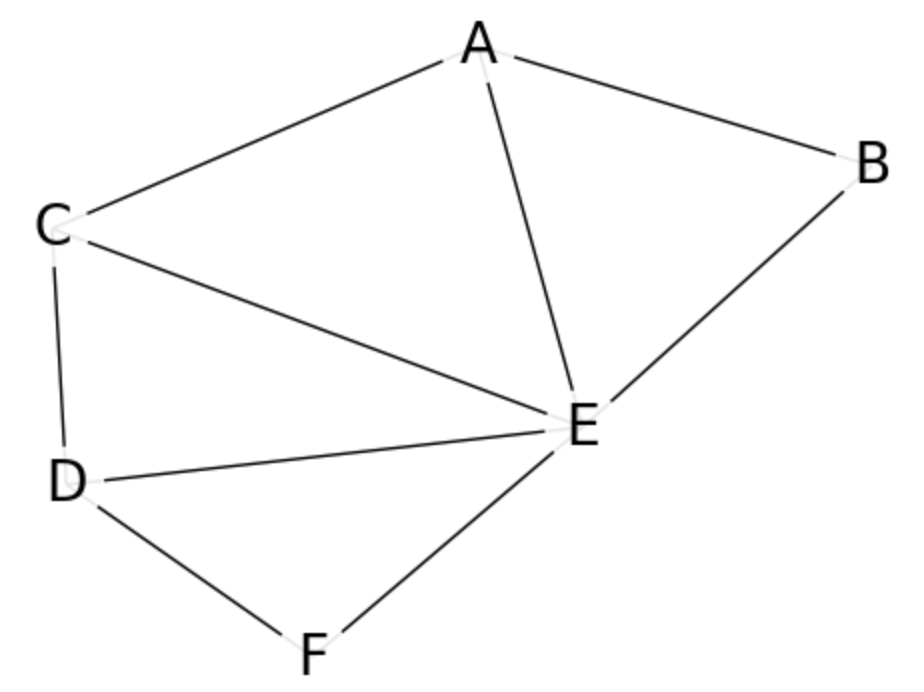
Interragir avec les attributs du graphe
L’objet graphe G possède des méthodes de type Getter et Setter. Nous allons explorer celles-ci.
Fonctions utiles de networkx
Pour connaitre la liste des sommets et des arêtes:
print(list(G.nodes()))
print(list(G.edges()))
La densité du graphe:
nx.density(G)
Pour connaitre la liste des voisins d’un sommet:
nx.neighbors(G,node)
Pour connaitre la liste des voisins de TOUS les sommets, ainsi que leur couleur:
for node in list(G.nodes()):
print(node,'->',list(nx.neighbors(G,node)),G.nodes(data='col')[node])
Q.c: Compléter le script pour obtenir le dictionnaire représentant ce graphe:
D = {}
for node in list(G.nodes()):
# a completer
print (D)
affiche:
{0: [1, 2, 4],
1: [0, 4],
2: [0, 4, 3],
3: [4, 2, 5],
4: [0, 1, 2, 3, 5],
5: [4, 3]}
Getter
La documentation de la fonction se trouve ici: networkx.org/documentation
Tester dans une nouvelle cellule:
color = nx.get_node_attributes(G, "col")
print('color',color)
Q.d: Quel est le format de données retourné par
get_node_attributes?
Q.e: Afficher la seule couleur du sommet 0, en modifiant cette instruction.
Q.f: Obtenir l’information des attributs label à l’aide d’une instruction similaire.
Setter
La documentation de la fonction se trouve ici: networkx.org/documentation
Tester dans une nouvelle cellule:
nx.set_node_attributes(G, {0:{"col":'blue'}})
color = nx.get_node_attributes(G, "col")
print('color',color)
Q.f: Que remarque t-on? Pourquoi?
Algorithmes de parcours de graphes
Pour une description illustrée de ces 2 parcours dans un graphe, on pourra consulter la page suivante sur le site allophysique.com.
La page suivante du site marcarea.com propose plusieurs implémentations pour les parcours en largeur et en profondeur d’un graphe.
-
Pour utiliser l’une de ces fonctions, il faudra une structure de données de type dictionnaire pour le graphe: revoir le paragraphe Fonctions utiles de networkx.
-
Ajouter une fonction pour dessiner et sauvegarder le graphe dans un fichier:
def dessine(G,filename):
plt.clf()
L = list(G.nodes(data='col'))
colorNodes = [node[1] for node in L]
nx.draw_networkx_nodes(G, pos, node_size=700, node_color=colorNodes, alpha=0.9)
# labels
labels_nodes = {node: label for node, label in G.nodes(data='label')}
nx.draw_networkx_labels(G, pos, labels=labels_nodes, \
font_size=20, \
font_color='black', \
font_family='sans-serif')
nx.draw_networkx_edges(G, pos)
plt.savefig(filename)
- Adapter ensuite la fonction de recherche pour tracer les graphes au fur et à mesure du parcours. Démarrer du sommet 0:
plt.figure() # utile pour afficher TOUS les graphes
recursive_dfs(D,0)
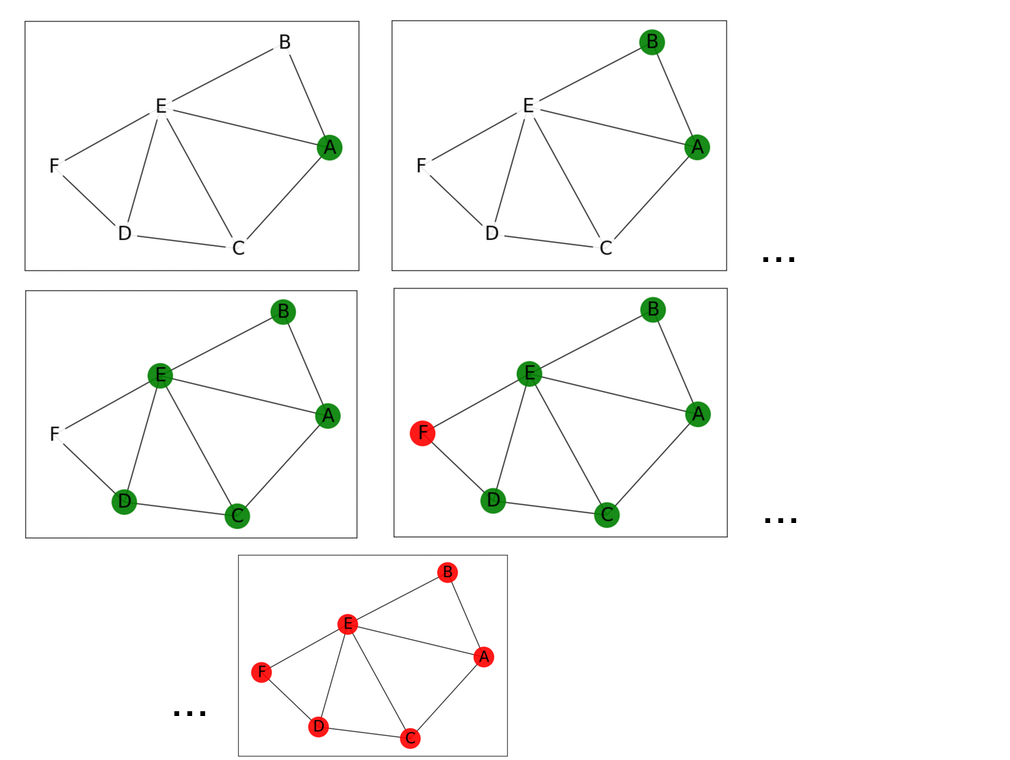
Correction
import matplotlib.pyplot as plt
import networkx as nx
from numpy import array
def inverse(L):
return [L[i] for i in range(len(L)-1,-1,-1)]
def dessine(G,filename):
plt.clf()
L = list(G.nodes(data='col'))
colorNodes = [node[1] for node in L]
nx.draw_networkx_nodes(G, pos, node_size=700, node_color=colorNodes, alpha=0.9)
# labels
labels_nodes = {node: label for node, label in G.nodes(data='label')}
nx.draw_networkx_labels(G, pos, labels=labels_nodes, \
font_size=20, \
font_color='black', \
font_family='sans-serif')
nx.draw_networkx_edges(G, pos)
plt.savefig(filename)
G = nx.Graph()
# definition des noeuds
G.add_node(0, label='A', col='white')
G.add_node(1, label='B', col='white')
G.add_node(2, label='C', col='white')
G.add_node(3, label='D', col='white')
G.add_node(4, label='E', col='white')
G.add_node(5, label='F', col='white')
# definition des aretes
G.add_edge(0, 1)
G.add_edge(0, 2)
G.add_edge(0, 4)
G.add_edge(4, 1)
G.add_edge(4, 2)
G.add_edge(4, 3)
G.add_edge(2, 3)
G.add_edge(4, 5)
G.add_edge(3, 5)
# calcul des positions pour repartir les sommets du graphe
pos = nx.spring_layout(G)
# Dictionnaire du graphe
D = {}
for node in list(G.nodes()):
D[node] = list(nx.neighbors(G, node))
print(D)
# Parcours en profondeur avec coloration des sommets
def dfs(graph, node, visited=None,stack=None):
compteur_image=0
if visited is None:
visited = []
if stack is None:
stack = []
stack.append(node)
nx.set_node_attributes(G, {node: {"col": 'green'}})
dessine(G, 'img/figure' + str(compteur_image) + '.png')
compteur_image+=1
while stack:
node = stack.pop()
if node not in visited :
#and G.nodes()[node]['col'] != 'red':
visited.append(node)
#plt.show()
unvisited = [n for n in graph[node] if n not in visited]
stack.extend(inverse(unvisited))
for n in unvisited :
nx.set_node_attributes(G, {n: {"col": 'green'}})
dessine(G, 'img/figure' + str(compteur_image) + '.png')
compteur_image += 1
nx.set_node_attributes(G, {node: {"col": 'red'}})
dessine(G,'img/figure'+str(compteur_image)+'.png')
compteur_image += 1
#plt.show()
return visited
# appel de dfs depuis le sommet 0 et affichage graphique
#plt.figure()
visited = dfs(D, 0)
print(visited)
Liens
- Documentation de python networkx
- Programmes python pour le parcours en largeur et en profondeur d’un graphe
- La sociologie structurale, appelée maintenant analyse de réseaux a développé une grande panoplie de métriques pour caractériser les réseaux sociaux… Mémoire de maitrise par FRANCK GOUDJO sur la Réalisation d’un outil de simulation de réseaux sociaux
