Transferts d’énergie

Energie

L’énergie désigne une capacité à modifier un état ou à produire un travail entraînant un mouvement ou générant un rayonnement électromagnétique - de la lumière, par exemple - ou de la chaleur.

Dans le système international, l’énergie s’exprime en joules (J). On note la grandeur Energie avec la lettre E ou Q. (Q est plutôt réservée pour l’énergie sous forme thermique)

Pas une mais des énergies

Stockée dans les objets, les molécules, les atomes, l’énergie se manifeste de multiples façons. Mais qu’elle soit mécanique, cinétique, électrique, thermique, chimique, rayonnante ou encore nucléaire, elle peut toujours se convertir d’une forme à une autre.

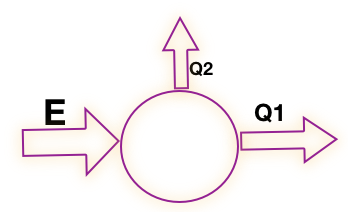
On représente ces transferts à l’aide d’une flèche =>, qui montre le sens de l’échange. Au départ ou à l’arrivée de cette flèche on dessine une forme (carré ou cercle) qui représente un sous système. Cette notion sera étudiée dans l’activité suivante.

Activité : transferts d’énergie

• Chargez et imprimez le document guide de cette activité

• Rendez vous à l’activité en ligne à l’adresse suivante : phet.colorado.edu energy-forms

• Choisir la page Systèmes.

• Utilisez la simulation et compléter le document.

Qu’avez vous appris de cette animation ? Vous avez certainement remarqué :

• que l’énergie prend de multiples formes dans la chaine énergétique complète.
• que l’énergie électrique peut être produite à partir de nombreuses énergies primaires. Souvent, c’est l’énergie mécanique qui est transformée en énergie électrique grâce à un ensemble turbine-alternateur. La turbine est l’élément qui est mis en rotation avec l’énergie mécanique.
• que lorsque l’on chauffe de l’eau, celle-ci gagne de l’énergie thermique (produite par l’énergie électrique), mais perd une partie de cette énergie thermique par vaporisation.

Les deux formes d’énergie thermique

Pourquoi deux formes ?

à l’échelle microscopique, les particules constituant la matière :

• ont un mouvement (de l’agitation). Leur énergie de mouvement est proportionnelle à leur température. On peut noter leur énergie avec une relation du type : (q1 : énergie microscopique; C : constante; T : température exprimée en Kelvin) $$q_1 = C\times T$$

Cette énergie est plus élevée si le corps est à une température plus élevée : il faut apporter de l’énergie pour augmenter sa température.

• sont en interactions entre elles, et soumises à des forces de contact et d’attraction ou répulsion mutuelle. Cette énergie q2 est plus basse dans les solides, où les forces d’attraction sont plus intenses que dans les liquides et les gaz : $$q_2{(solide)} < q_2{(liquide)} < q_2{(gaz)}$$

Cette énergie est plus élevée pour les milieux moins condensés : le gaz est le moins condensé et a une énergie q2 plus élevée. Il faut alors fournir de l’énergie à un système Liquide pour l’amener à l’état Gaz.

Comment quantifier ces échanges thermiques ?

A l’échelle macroscopique (notre échelle, celle où nous pouvons réaliser des mesures de température), nous allons quantifier (calculer) les variations de ces énergies à l’aide des 2 lois suivantes :

variation d’énergie thermique liée à une variation de température

(et sans changement d’état)

Définition : Soit un corps de masse m, de capacité thermique c, dont la température varie de T1 (initiale) à T2 (finale), alors la variation d’énergie thermique Q de ce corps est : $$Q = m \times c \times (T_2 - T_1)$$

Cette loi est aussi appelée : loi de calorimétrie.

Exemple : On considère un système constitué de 1,00kg d’eau, pris initialement à la température T1 = 20,0°C. Quelle quantité d’énergie Q faut-il fournir pour amener toute cette quantité d’eau jusqu’au point d’ébullition (T2 = 100°C) ?. $$c_{eau} = 4180 J.kg^{-1}.K^{-1}$$

Réponse : D’après la loi de calorimétrie : $$Q = m \times c \times (T_2 - T_1) = 1,00 \times 4180 \times (100-20,0)$$ $$Q = 334000J = 334 kJ$$

Gain ou perte d’énergie : Comme il s’agit d’un échange, le système reçoit ou cède de l’énergie:

• Si T2 > T1, alors la quantité Q est positive. Alors le système reçoit de l’énergie thermique.
• Si T1 < T2, alors la quantité Q est négative. Alors le système cède de l’énergie thermique.

variation d’énergie thermique liée à un changement d’état

(et pour un corps pur, sans variation de température)

Définition :

Lorsqu’un corps de masse m subit une transformation physique, qui l’amène à changer complètement d’état, alors il échange une énergie Q : $$Q = m\times L$$

L est la chaleur latente, et dépend du corps ET du type de changement d’état.

Quelques valeurs de chaleur latente, en kJ/kg :

Remarques :

• Les chaleurs latentes des transformation opposées sont égales, mais de signe contraire : L(fusion) = - L(solidification) et L(vap) = -L(liquef)
• La valeur de L est positive lorsque le changement d’état se fait d’un état condensé vers un état moins condensé. Cela signifie qu’il faut APPORTER de l’énergie pour réaliser la transformation vers un état moins condensé. (endo)
• La valeur de L est négative lorsque le changement d’état se fait d’un état moins condensé vers un état plus condensé. C’est alors le corps qui cède de l’énergie vers l’exterieur. (exo)

Définitions : ENDO/EXO thermique

• Une transformation est exothermique lorsque le système céde de l’énergie vers l’exterieur. C’est le cas des transformations physiques vers des états plus condensés (liquefaction G => L et solidification L => S). La valeur de Q = m.L est négative.
• Une transformation est endothermique lorsque le système prélève de l’énergie de l’exterieur. C’est le cas des transformations physiques vers des états moins condensés (vaporisation L => G et fusion S => L). La valeur de Q = m.L est positive.

Exercice : Calculer l’énergie thermique qu’il faut apporter à 2,0L d’eau liquide, pris à 100°C pour tout vaporiser. (L=2257kJ/kg)

Réponse : D’après la valeur de masse volumique de l’eau : V = 2,0 L correspond à m = 2,0kg.

$$Q = m\times L(vap) = 2,0 \times 2257 = 4500 kJ$$

L’énergie cinétique

Définition :

C’est l’énergie que possède un corps du fait de son mouvement par rapport à un référentiel donné. Sa valeur dépend donc du choix de ce référentiel.

Pour un corps de masse m (kg), et de vitesse v (en m/s), l’énergie cinétique E, en Joules, vaut :

$$E = \tfrac{1}{2} \times m \times v^2$$

L’énergie cinétique est une forme de l’énergie mécanique.

Exercice : Calculer la valeur de l’énergie cinétique pour un autobus (m = 19000 kg, passagers compris) roulant à la vitesse v = 36,5 km/h.

Reponse : $$v = 36,5km.h^{-1} = \tfrac{36,5}{3,6} = 10,1 m.s^{-1}$$ $$E = \tfrac{1}{2} \times m \times v^2 = \tfrac{1}{2} \times 19000 \times 10,1^2$$ $$E = 9,7.10^5 J$$

Remarque : La contribution à l’énergie de la vitesse est beaucoup plus importante que celle de la masse (v au carré).